In an earlier article, I covered the basic technique for performing matrix-vector multiplication in fully homomorphic encryption (FHE), known as the Halevi-Shoup diagonal method. This article covers a more recent method for matrix-matrix multiplication known as the bicyclic method.
The code implementing this method is in the same GitHub repository as the previous article, and the bicyclic method is in a file called bicyclic.py.
The previous article linked above covers the general concepts behind “FHE packing,” which I will assume as background knowledge for this article:
- The “abstract” computational model of SIMD-style FHE (CKKS, BGV, BFV) involving ciphertexts represented as large-width vectors of slots, with elementwise additions, multiplications, and rotations as elementary operations.
- The conjoined duties of packing data into ciphertexts (akin to memory layout) and deciding what circuit of elementary operations operates on that packing to implement the functionality equivalent to the desired cleartext operation.
- The efficiency metrics: small multiplicative depth, few rotation operations, and the ability to batch rotations on the same ciphertext (hoisting).
The bicyclic method
The bicyclic method was introduced in the paper Homomorphic Matrix Operations under Bicyclic Encoding by Jingwei Chen, Linhan Yang, Wenyuan Wu, Yang Liu, and Yong Feng. I first heard about it via an extension of the technique to support batch matrix-matrix multiplication in Tricycle: Private Transformer Inference with Tricyclic Encodings by Lawrence Lim, Vikas Kalagi, Divyakant Agrawal, and Amr El Abbadi.
The technique also involves a diagonal-like packing similar to the Halevi-Shoup method, and as a result it enjoys many of the same benefits:
- A minimal multiplicative depth of 1.
- Layout-invariant, meaning the output is packed according to the same algorithm as the input (modulo differences in matrix dimensions).
- A number of rotations that scales linearly with the matrix dimension, though lower-level tricks (Baby-Step-Giant-Step, for another post) reduce that to more like a square-root growth.1
The packing of a matrix is defined as follows:
Definition: Given an $m \times n$ matrix $A = (a_{i, j})$, and a ciphertext with $N$ slots, the bicyclic packing of $A$ is the length-$N$ vector $\varphi(A)$ defined by
$$ \varphi(A)_k = a_{k \textup{ mod } m, k \textup{ mod } n} $$This packing can be used for any values of $m, n$, but the matrix multiplication kernel is only valid if, for two matrices $A$ of size $m \times n$ and $B$ of size $n \times p$, the axis sizes $m, n, p$ are all coprime.
Example: The bicyclic encoding with $N=15$ slots for the matrix
$$ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\\ 6 & 7 & 8 & 9 & 10 \\\ 11 & 12 & 13 & 14 & 15 \end{pmatrix} $$is
$$ (1, 7, 13, 4, 10, 11, 2, 8, 14, 5, 6, 12, 3, 9, 15) $$Recall that the divisibility condition from the Halevi-Shoup kernel ensured that, when diagonals wrapped around the edges of the matrix, they wouldn’t overlap with other diagonals. By contrast, the bicyclic coprimality condition ensures that one long wrapping diagonal traverses every entry of the matrix.
The packing code here is straightforward:
def pack(matrix: list[list[int]], num_slots: int) -> Ciphertext:
rows, cols = len(matrix), len(matrix[0])
if gcd(rows, cols) != 1:
raise ValueError(...)
data = [matrix[k % rows][k % cols] for k in range(rows * cols)]
while len(data) < num_slots:
# duplicate the data until it fills the slots
data += data
# truncate to the exact slot size
return Ciphertext(data[:num_slots])
The replication at the end is actually important. Two multiplicand matrices $A$ of shape $m \times n$ and $B$ of shape $n \times p$ will have different sizes in general, and the rotations used in the kernel will extend beyond $mn$ and $np$.2
The unpacking, naturally, uses the Chinese Remainder Theorem to get from the desired matrix entry to the corresponding slot index.
def unpack(encoded: Ciphertext, m: int, n: int) -> list[list[int]]:
if gcd(m, n) != 1:
raise ValueError(...)
matrix = [[0] * n for _ in range(m)]
n_inv_mod_m = pow(n, -1, m) # n^{-1} mod m
m_inv_mod_n = pow(m, -1, n) # m^{-1} mod n
for i in range(m):
for j in range(n):
k = (i * n * n_inv_mod_m + j * m * m_inv_mod_n) % (m * n)
matrix[i][j] = encoded.data[k]
return matrix
In particular (this formula will be useful in the next step), for a matrix $A$ of size $m \times n$, the value at $a_{i, j}$ is in slot
$$ a_{i, j} \mapsto \varphi(A)_{i n (n^{-1} \textup{ mod } m) + j m (m^{-1} \textup{ mod } n) \textup{ mod } (m n)} $$Now, given two matrices $A$ and $B$ packed using the bicyclic method, let’s derive the matrix multiplication kernel. Let $A$ have size $m \times n$ and $B$ have size $n \times p$. The matrix product $C = AB$ has size $m \times p$ with entries
$$ c_{i, j} = \sum_{k=0}^{n-1} a_{i, k} b_{k, j} $$Our general kernel structure will be as follows:
- In a loop of size $n$:
- Rotate the encoded $\varphi(A)$ and $\varphi(B)$ matrices by some amounts (possibly different for $A$ and $B$)
- Multiply the rotated ciphertexts elementwise.
- Sum up all the resulting ciphertexts.
This structure is reasonably necessary, at least in the sense that each entry of the output matrix $c_{i, j}$ has $n$ summands, but each elementwise product only computes one summand per slot. So without repeating the matrix entries more than $O(1)$ times, we will need $\Theta(n)$ ciphertext-ciphertext multiplications and $\Theta(n)$ rotations to collect all the terms. The question is whether we can do this without any waste.
Indeed we can, and to derive the required rotations, we notice that, when computing a matrix multiplication, the inner contraction index (the $k$ in $a_{i, k} b_{k, j}$) walks rightward across a row of $A$ while walking downward along a column of $B$.
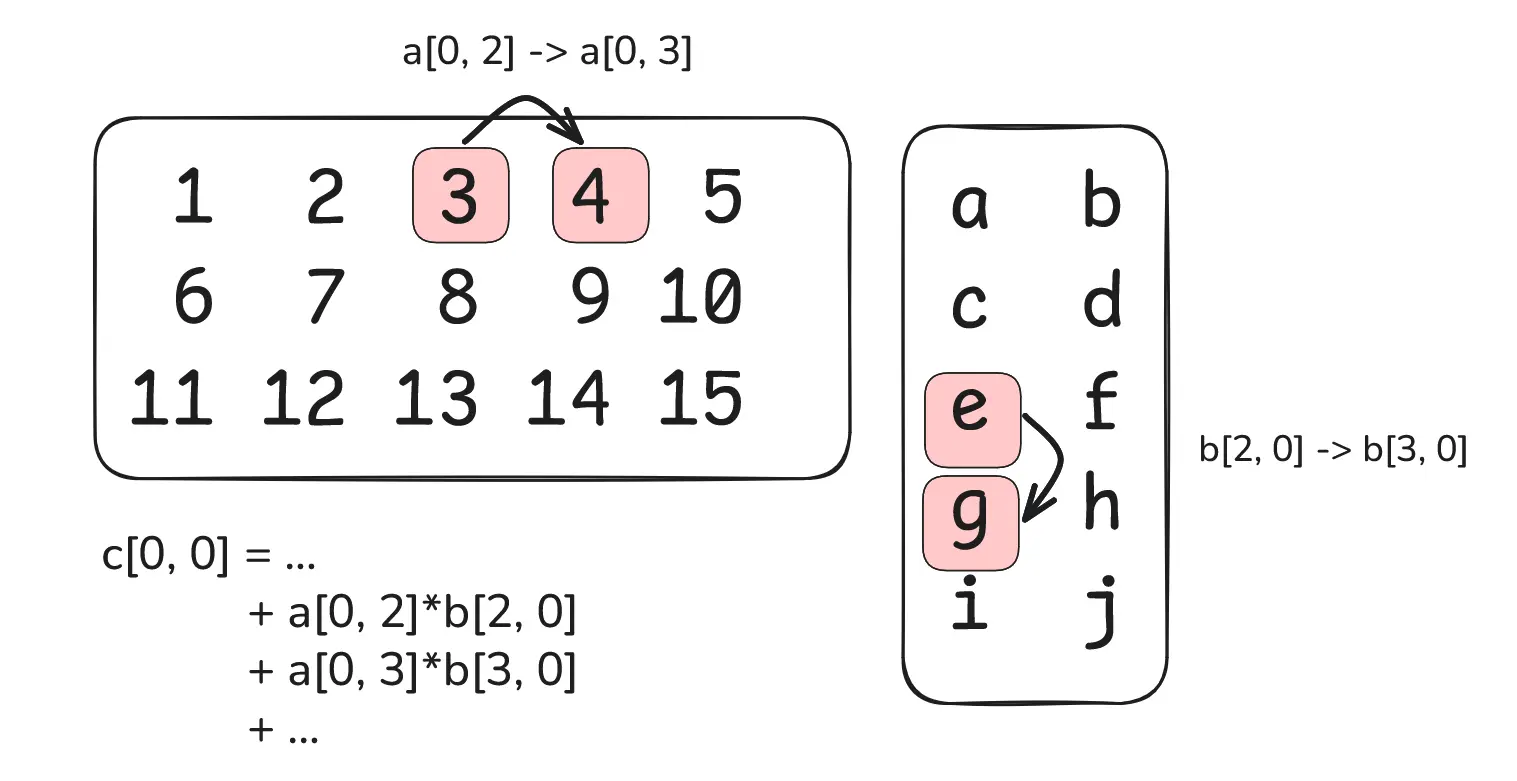
Setting up the punchline: showing how to terms of one matmul output entry are adjacent by column and row (trivial).
So the rotations we need for $A$ and $B$ should correspond to the difference between the slot positions when going from $(i, k)$ to $(i, k+1)$ for $A$ and from $(k, j)$ to $(k+1, j)$ for $B$.
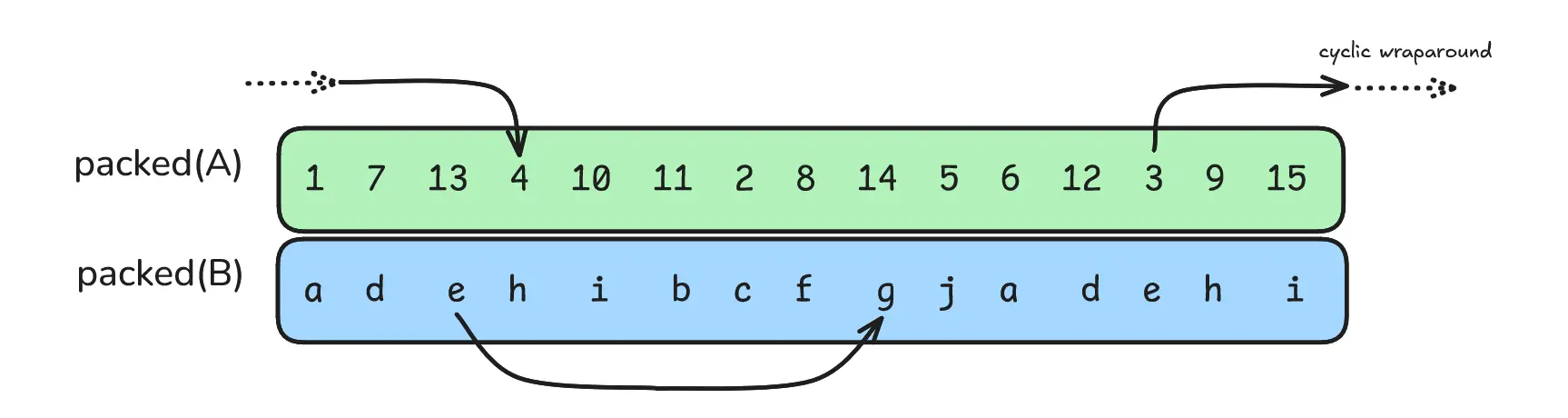
Continuing from the figure above, the 3x5 matrix $A$ is packed on top, the 5x2 matrix $B$ on bottom, and the arrows show the gap between the adjacent slots that must be aligned. The fact that both rotations are 6 is a coincidence: $2 \cdot (2^{-1} \textup{ mod } 5)$ happens to equal $3 \cdot (3^{-1} \textup{ mod } 5)$. Notice also that the shifts for all values in the first row (1->2->3->4->5) are the same, as are the shifts for all values in the first column (a->c->e->g->i). The chosen entries (3/e and 4/g) appear misaligned, but relative to their respective moduli ($mn$ and $np$) they are aligned, and you can see that by noticing the 3 from the top is aligned with a (repetition of) an e on the bottom.
Using the formula above for slot indices, we compute these differences and notice that they are actually independent of the indices $i$ and $j$. This is the key property that makes this kernel work: the same set of rotations for $\varphi(A)$ and $\varphi(B)$ is valid to accumulate the corresponding summands for all desired $c_{i, j}$.
For $A$ (of shape $m \times n$), we have:
$$ \begin{aligned} a_{i, j} \mapsto \varphi(A)_{i n (n^{-1} \textup{ mod } m) + j m (m^{-1} \textup{ mod } n) \textup{ mod } (m n)} \\ a_{i, j+1} \mapsto \varphi(A)_{i n (n^{-1} \textup{ mod } m) + (j+1) m (m^{-1} \textup{ mod } n) \textup{ mod } (m n)} \\ \end{aligned} $$Subtracting the first slot from the second slot simplifies to
$$ r_A := m (m^{-1} \textup{ mod } n) \textup{ mod } (m n) $$Likewise for $B$ (of shape $n \times p$), we have:
$$ \begin{aligned} b_{i, j} \mapsto \varphi(B)_{i p (p ^{-1} \textup{ mod } n) + j n (n^{-1} \textup{ mod } p) \textup{ mod } (n p)} \\ b_{i+1, j} \mapsto \varphi(B)_{(i +1) p (p^{-1} \textup{ mod } n) + j n (n^{-1} \textup{ mod } p) \textup{ mod } (n p)} \\ \end{aligned} $$And the difference simplifies to
$$ r_B := p (p^{-1} \textup{ mod } n) \textup{ mod } (n p) $$Since these $r_A, r_B$ are independent of $i, j$, it’s the same relative shift for each step in the summation of terms contributing to $c_{i, j}$. The needed value of $c_{i, j}$ can be computed by summing:
$$ \sum_{k=0}^{n-1} \textup{rot}(\varphi(A), kr_A) \cdot \textup{rot}(\varphi(B), kr_B) $$And again, since the rotations are independent of $i, j$, this single summation works for all entries of the output matrix $C$ simultaneously. The final kernel code is as follows:
def matrix_multiply(
packed_matrix_a: Ciphertext,
packed_matrix_b: Ciphertext,
m: int,
n: int,
p: int,
) -> Ciphertext:
assert pairwise_coprime(m, n, p), "Dimensions must be pairwise coprime."
assert len(packed_matrix_a) == len(
packed_matrix_b
), "Both ciphertexts must have the same number of slots"
result = Ciphertext([0] * len(packed_matrix_a))
m_inv_mod_n = pow(m, -1, n)
p_inv_mod_n = pow(p, -1, n)
for k in range(n):
a_rot = k * m * m_inv_mod_n % (m * n)
b_rot = k * p * p_inv_mod_n % (n * p)
rotated_a = packed_matrix_a.rotate(a_rot)
rotated_b = packed_matrix_b.rotate(b_rot)
prod = rotated_a * rotated_b
# One should accumulate these in a tree-like fashion for optimal
# noise growth, but this is just a blog post.
result += prod
return result
As with the Halevi-Shoup kernel, because many rotations are applied to the same input ciphertext, they can be hoisted to share some common computation related to the NTT calculations that implement the rotation in the cryptosystem.
Reflections and extensions
It’s worth a moment to reflect on the conditions required to make this matmul kernel work. First, since all the matrix dimensions need to be coprime, one must in general pad the matrices with one or two rows or columns of zeros to achieve this. In general this is a minor inefficiency.
Second, the method requires replicating the packed matrices enough so that they can stay aligned with the corresponding slots of the largest of the three matrices involved: the two input matrices of sizes $mn$ and $np$, and the output matrix of size $mp$. For example, an input $11 \times 2$ matrix $A$ and an input $2 \times 13$ matrix $B$ results in an output $11 \times 13$ matrix $C$, so both input matrices need to be replicated to fill at least $11 \cdot 13$ slots. This effectively forces the number of slots you need to be at least $2\max(mn, np, mp)$.
Finally, the fact that a matrix must be packed entirely in a single ciphertext limits the size of the matrices you can multiple. For example, typical FHE schemes use something like $N=2^{15}=32768$ slots, which means you cannot multiply two 256-by-256 matrices using this method. For larger matrices, the Bicyclic paper proposes using the classical block matrix-multiplication, as well as a different algorithm (BMM-III) that trades off multiplicative depth for supporting larger matrices. To my knowledge, better support for large matrix multiplication in FHE is still an open research area.
That said, the Tricycle paper mentioned at the beginning of this article adds some nice extensions to this method, for the purpose of implementing transformer models in FHE:
- Supporting batch matrix-matrix multiplication, as well as other variants like “concatenated” matrix multiplication. (Hence “tricyclic” for wrapping around all three dimensions)
- Supporting ciphertext-plaintext matrix multiplication where the plaintext matrix is not constrained by the coprimality condition, the size limitations, or the replication requirement that halves the number of usable slots.
- Using the so-called Baby-Step Giant-Step technique to reduce the total number of rotations requried (the size of the reduction differs in the ciphertext-ciphertext case vs the ciphertext-plaintext case).
Thanks to Lawrence Lim for feedback on a draft of this article.
I recently heard about a paper Shane Kosieradzki and Hannah Mahon where they presented a matrix multiplication packing scheme that improves by requiring only $O(\log n))$ rotations for $n \times n$ matrices (similar to the Bicyclic paper’s BMM-II). However, their method requires a non-standard ring structure for the underlying RLWE problem. Another paper By Craig Gentry and Yongwoo Lee, which I’m still working through, uses another nonstandard (multivariate) ring structure and an entirely new FHE scheme that natively supports matrix multiplication. Suffice it to say I’ll have a future blog post on that method. ↩︎
While the code in this repository replicates so as to completely fill the available slots, that is not necessary. Some replication is required to keep the matmul correct, but after the minimum required replication, any remaining slots can be left as zero. ↩︎
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.
This article is syndicated on: