In my recent overview of homomorphic encryption, I underemphasized the importance of data layout when working with arithmetic (SIMD-style) homomorphic encryption schemes. In the FHE world, the name given to data layout strategies is called “packing,” because it revolves around putting multiple plaintext data into RLWE ciphertexts in carefully-chosen ways that mesh well with the operations you’d like to perform. By “mesh well” I mean it reduces the number of extra multiplications and rotations required merely to align data elements properly, rather than doing the actual computation you care about. Packing is an advanced topic, but it’s critical for performance and close to the cutting edge of FHE research.
Among this topic lie three sort of sub-problems:
- How do you design a good packing for a particular operation or subset of a program? (This article)
- How do you convert between packings once they have been established? (see shift networks)
- How do you holistically optimize for the right packing choices across an entire program, when considering the savings from choosing good packings, the cost of switching, and the profile of operations performed?
This article is about the first problem: how do you design a packing? I’ll cover two basic packing techniques for matrix-vector multiplication. I would like this article to serve as a warm up to other articles covering more advanced packing techniques. Code for this article is available in a GitHub repository.
To start, we need to provide a rough interface for the computational model.
The Computational Model
The SIMD-style FHE computational model is loosely summarized as follows.
- Data is stored in one or more vectors of a fixed length (e.g., 4096) and fixed bit precision (e.g., 16 bits). The vectors are RLWE ciphertexts, but the computational model can be studied without caring much about how the encryption works.
- You can apply elementwise addition or multiplication on the vectors.
- You can cyclically rotate the vectors by a statically-known shift.
- Multiplication is very expensive, rotation is somewhat expensive, addition is cheap.
- While multiplication is expensive, parallel multiplications are best. In other words, when multiplication is necessary, parallel element-wise multiplication ops are better than data-dependent serial multiplications (i.e., aim for “low multiplicative depth”).
To go along with this, I implemented a simple Python object that represents the computational model. Rather than realistically implement an FHE scheme, it merely limits the API to the allowed operations. The file computational_model.py contains a class that limits the API to the allowed operations, ignoring limitations on bit precision for clarity.
class Ciphertext:
def __init__(self, data: list[int]):
self.data = data[:]
self.dim = len(data)
def __add__(self, other: "Ciphertext") -> "Ciphertext":
assert self.dim == other.dim
return Ciphertext([self.data[i] + other.data[i] for i in range(len(self.data))])
def __mul__(self, other) -> "Ciphertext":
if isinstance(other, Ciphertext):
assert self.dim == other.dim
return Ciphertext([self.data[i] * other.data[i] for i in range(len(self.data))])
elif isinstance(other, list):
# Plaintext-ciphertext multiplication
assert self.dim == len(other) and isinstance(other[0], int)
return Ciphertext([x * y for (x, y) in zip(self.data, other)])
elif isinstance(other, int):
# Plaintext-ciphertext multiplication
return Ciphertext([other * x for x in self.data])
def rotate(self, n: int) -> "Ciphertext":
n = n % self.dim
return Ciphertext(self.data[-n:] + self.data[:-n])
... (other helpers) ...
The essential problem behind packing conversion is that once data is laid out in an encrypted ciphertext, there is no elementary “shuffle” operation to permute data around. So if you want to do an elementwise addition or multiplication, and your inputs aren’t aligned properly, you have to use rotations, multiplications, and additions to align them, and these operations have nontrivial costs.
Halevi-Shoup Diagonal Matrix Packing
In this packing, the goal is to perform a matrix-vector multiplication $Ax = y$. The matrix $A$ is cleartext while $x$ and $y$ are encrypted, so we need to decide how to pack the matrix entries into ciphertexts to allow us to do matrix multiplication in this computational model.
First we’ll spend a bunch of effort to write down the naive baseline approach to this problem.
Naive approach
The naive approach, sometimes called row packing, is to encode each row of the matrix in its own ciphertext. For each row $i$, pack row $A_i$ into ciphertext $z_i$, then compute the elementwise product $z_i \cdot x$ for each $i$.
\[ \begin{pmatrix} a_{0,0} & a_{0,1} & \cdots & a_{0,n-1} \\ a_{1,0} & a_{1,1} & \cdots & a_{1,n-1} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n-1,0} & a_{n-1,1} & \cdots & a_{n-1,n-1} \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ \vdots \\ x_{n-1} \end{pmatrix} \] \[ \downdownarrows \] \[ \begin{aligned} z_0 \otimes x &= (a_{0, 0} x_0, a_{0, 1} x_1, \ldots, a_{0, n-1} x_{n-1}) \\ z_1 \otimes x &= (a_{1, 0} x_0, a_{1, 1} x_1, \ldots, a_{1, n-1} x_{n-1}) \\ & \hspace{0.5em} \vdots \\ z_{n-1} \otimes x &= (a_{n-1, 0} x_0, a_{n-1, 1} x_1, \ldots, a_{n-1, n-1} x_{n-1}) \\ \end{aligned} \]Above I use $\otimes$ (LaTeX \otimes) to denote elementwise multiplication.
The resulting vectors need to be summed to get each entry of $y_i$, and then the summed vectors need to be placed in the appropriate position in the output vector. This shows the downside of this packing. To sum the entries of a vector, you need the “rotate and sum” trick, which involves $\log_2(n)$ rotations and additions. In Python, this looks like
def rotate_and_sum(ciphertext):
n = len(ciphertext)
assert is_power_of_two(n)
result = ciphertext.copy()
shift = n // 2
while shift > 0:
result += result.rotate(shift)
shift //= 2
return result
This produces a vector where each entry is the sum of all the entries in the input vector. Let $y_i = \sum_{j=0}^{n-1} a_{i,j} x_j$. Then after reducing each row-product we get the following $n$ vectors:
\[ \begin{aligned} (y_0, y_0, &\dots, y_0) \\ (y_1, y_1, &\dots, y_1) \\ &\hspace{0.5em} \vdots \\ (y_{n-1}, y_{n-1}, &\dots, y_{n-1}) \\ \end{aligned} \]To combine these, we need to mask out the appropriate entries by multiplying by a one-hot vector. This incurs an additional linear number of multiplications, but then we can finally sum them up.
\[ \begin{aligned} Ax &= (y_0, y_0, \dots, y_0) \otimes (1, 0, \dots, 0) \\ &+ (y_1, y_1, \dots, y_1) \otimes (0, 1, \dots, 0) \\ &+ \dots \\ &+ (y_{n-1}, y_{n-1}, \dots, y_{n-1}) \otimes (0, 0, \dots, 1) \\ \end{aligned} \]In all, this method requires $2n$ multiplications, and $n \log_2(n)$ rotations, and the multiplicative depth is 2.
Actual Halevi-Shoup
The Halevi-Shoup method, which is described in section 4.3 of this paper as “the parallel ‘systolic’ multiplication algorithm”1, uses a different ordering of the matrix entries (still among $n$ ciphertexts) to reduce the number of multiplications and rotations required. It packs matrix entries along wrapping sub-diagonals, and rotates the input vector differently for each before doing the elementwise product. Then the result can be summed directly. As such, it is more colloquially called “the diagonal method.”
In detail, for an $n \times n$ matrix, we have $n$ ciphertexts, and we store in ciphertext $i$ and index $j$ the value $a_{j, (i+j) \textup{ mod } n}$.
\[ \begin{pmatrix} a_{0,0} & a_{0,1} & \cdots & a_{0,n-1} \\ a_{1,0} & a_{1,1} & \cdots & a_{1,n-1} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n-1,0} & a_{n-1,1} & \cdots & a_{n-1,n-1} \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ \vdots \\ x_{n-1} \end{pmatrix} \] \[ \downdownarrows \] \[ \begin{aligned} z_0 &= (a_{0, 0}, a_{1, 1}, \dots, a_{n-1, n-1}) \\ z_1 &= (a_{0, 1}, a_{1, 2}, \dots, a_{n-1, 0}) \\ & \hspace{0.5em} \vdots \\ z_{n-1} &= (a_{0, n-1}, a_{1, 0}, \dots, a_{n-1, n-2}) \\ \end{aligned} \]You can picture this as follows for $n = 4$:
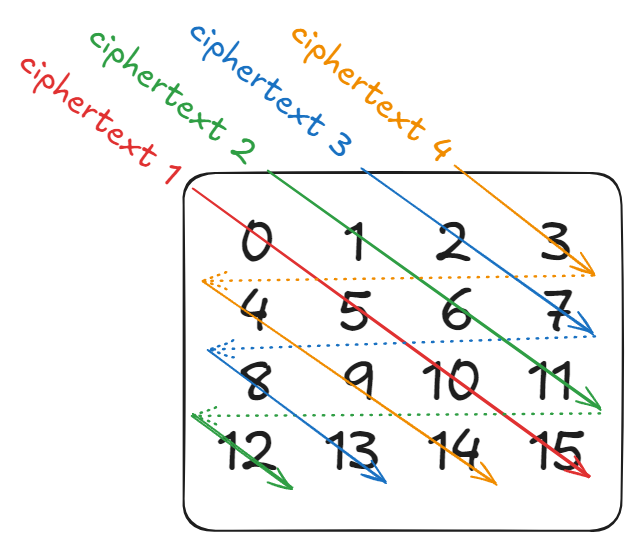
Halevi-Shoup diagonal packing example for $n=4$
In code (simplified slightly from halevi_shoup.py):
def pack(matrix):
"""Pack the matrix into a list of ciphertexts via Halevi-Shoup."""
# only square matrices for this demo
assert len(matrix) == len(matrix[0])
n = len(matrix)
ciphertexts = [[None] * n for _ in range(n)]
for i in range(n):
for j in range(n):
ciphertexts[i][j] = matrix[j][(i + j) % n]
return [Ciphertext(ciphertexts[i]) for i in range(n)]
Then each elementwise product is computed as $z_i \otimes \textup{rot}(x, -i)$
\[ \begin{aligned} z_0 \otimes \textup{rot}(x, -0) &= (a_{0, 0} x_0, a_{1, 1} x_1 , \dots, a_{n-1, n-1} x_{n-1}) \\ z_1 \otimes \textup{rot}(x, -1) &= (a_{0, 1} x_1, a_{1, 2} x_2 , \dots, a_{n-2, n-1} x_{n-1}, a_{n-1, 0} x_0) \\ & \hspace{0.5em} \vdots \\ z_{n-1} \otimes \textup{rot}(x, -(n-1)) &= (a_{0, n-1} x_{n-1}, a_{1, 0} x_0 , \dots, a_{n-1, n-2} x_{n-2}) \\ \end{aligned} \]Summing these vectors gives the correct result. See how the first column gives $y_0 = \sum_j a_{0, j} x_j$, and each subsequent row gives the appropriate sum, but the terms are cyclically rotated by one more each time.
In code (simplified slightly from halevi_shoup.py):
def matrix_vector_multiply(packed_matrix, vector):
n = len(packed_matrix)
row_products = []
for i in range(n):
# packed ciphertext i * vector rotated by -i
row_products.append(packed_matrix[i] * vector.rotate(-i))
# Sum the results together
result = row_products[0]
for i in range(1, n):
result += row_products[i]
return result
Altogether, this method requires only $n$ multiplications and $n$ rotations, and the multiplicative depth is 1.
Aside: “hoisting”
The paper Juvekar-Vaikuntanathan-Chandrakasan 2018 describes the Halevi-Shoup method as particularly helpful for a technique called hoisting (which I don’t yet understand). In particular, Halevi-Shoup ensures all the rotations involved in a matrix-vector product are applied to the same (input) ciphertext. In this setting, hoisting allows one to more efficiently compute a large number of rotations by factoring out some computation (an inverse NTT) common to all of them.
This gives an extra incentive to shift any rotation operations to the input to a computation.
Squat Diagonal Matrix Packing
The squat diagonal packing is a variant of the Halevi-Shoup diagonal packing for matrices with a small number of rows. This method comes from Juvekar-Vaikuntanathan-Chandrakasan 2018 (they call it the “hybrid” method, but I think “squat diagonal” is more memorable). There, the motivation is to have more efficient matrix-vector multiplications implementing fully-connected neural network layers. These matrices often have smaller output dimensions than input dimensions, and so this method shows how one can pack more of the matrix into fewer ciphertexts.
The method generalizes Halevi-Shoup diagonal packing by wrapping around the bottom of the matrix as well as the right side.
First in notation. For an $n \times m$ matrix with $n < m$, we have $n$ ciphertexts, and in ciphertext $i$ and index $j$ we store the value $a_{j \textup{ mod } n, (i+j) \textup{ mod } m}$. Note this requires both dimensions be powers of two.2
This is one of those definitions best shown by example.
\[ \begin{pmatrix} a_{0,0} & a_{0,1} & a_{0,2} & a_{0,3} & a_{0,4}& a_{0,5}& a_{0,6}& a_{0,7}\\ a_{1,0} & a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4}& a_{1,5}& a_{1,6}& a_{1,7}\\ a_{2,0} & a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4}& a_{2,5}& a_{2,6}& a_{2,7}\\ a_{3,0} & a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4}& a_{3,5}& a_{3,6}& a_{3,7}\\ \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ \end{pmatrix} \] \[ \downdownarrows \] \[ \begin{aligned} z_0 &= (a_{0, 0}, a_{1, 1}, a_{2, 2}, a_{3, 3}, a_{0, 4}, a_{1, 5}, a_{2, 6}, a_{3, 7}) \\ z_1 &= (a_{0, 1}, a_{1, 2}, a_{2, 3}, a_{3, 4}, a_{0, 5}, a_{1, 6}, a_{2, 7}, a_{3, 0}) \\ z_2 &= (a_{0, 2}, a_{1, 3}, a_{2, 4}, a_{3, 5}, a_{0, 6}, a_{1, 7}, a_{2, 0}, a_{3, 1}) \\ z_3 &= (a_{0, 3}, a_{1, 4}, a_{2, 5}, a_{3, 6}, a_{0, 7}, a_{1, 0}, a_{2, 1}, a_{3, 2}) \\ \end{aligned} \]Then as a picture:
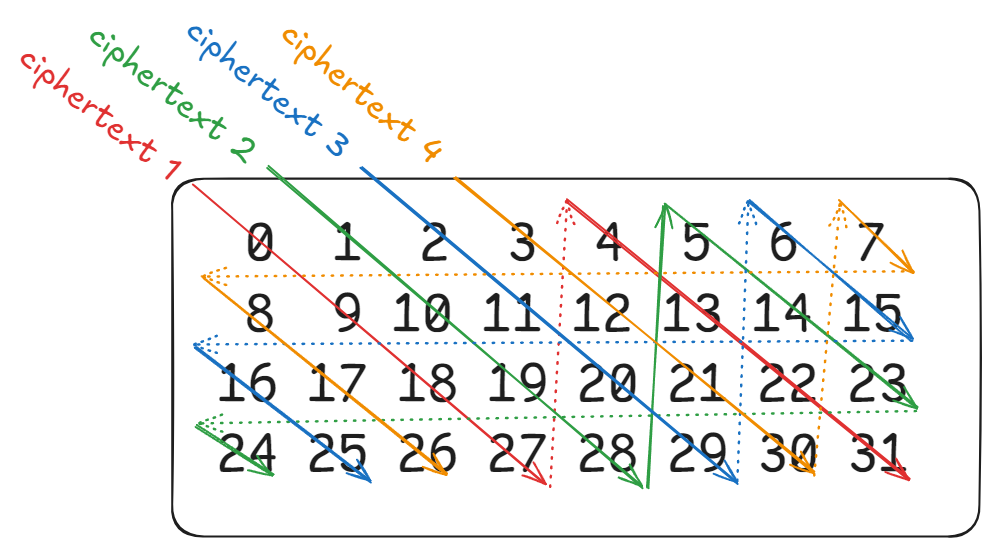
Squat diagonal packing example for $n=4, m=8$
Then in code (also in halevi_shoup.py, to contrast with the Halevi-Shoup packing):
def pack_squat(matrix):
"""Pack the matrix into a list of ciphertexts via
Juvekar-Vaikuntanathan-Chandrakasan squat diagonal packing.
"""
n, m = len(matrix), len(matrix[0])
ciphertexts = [[None] * m for _ in range(n)]
for i in range(n):
for j in range(m):
ciphertexts[i][j] = matrix[j % n][(i + j) % m]
return [Ciphertext(ciphertexts[i]) for i in range(n)]
The rest of the computation is similar to Halevi-Shoup, with one extra step. Once you sum the per-row elementwise products, you get a vector with two problems. First, it’s the wrong dimension. In the $4 \times 8$ example above, this intermediate output vector has size 8. Second, each entry contains only a partial sum of the terms in the desired output entry. In the $4 \times 8$ matrix example above, the first entry of $\sum_{i=0}^4 z_i \otimes x$ contains only the first four entries of the output: $a_{0, 0} x_0 + a_{0, 1} x_1 + a_{0, 2} x_2 + a_{0, 3}x_3$. The remaining four terms are at index 5.
The first problem cannot really be reconciled. The cryptosystem requires the ciphertexts have the same power of two dimension throughout, and the input vector is already dimension 8 (in the example), so the output of the matrix-vector multiplication must also be dimension 8, even though the matrix-vector product naturally has dimension 4.3 What you can do, however, is mask out the first four terms (zero out the last four). This produces a more “sparsely packed” ciphertext, which is less efficient. More advanced packing methods have ways to compensate for this.
The second problem is more easily solved by doing a partial rotate-and-sum trick. This works because the squat-diagonal packing’s wrap-around ensures that the terms you need to combine are equidistantly spaced in the intermediate vector.
In code, the matrix-vector product is implemented as:
def matrix_vector_multiply_squat(packed_matrix, vector):
"""Multiply the squat-diagonal-packed matrix by the vector."""
n, m = len(packed_matrix), len(packed_matrix[0])
# Same as Halevi-Shoup
row_products = []
for i in range(n):
row_products.append(packed_matrix[i] * vector.rotate(-i))
# Same as Halevi-Shoup
partial_sums = row_products[0]
for i in range(1, n):
partial_sums += row_products[i]
# The rest is specific to the squat packing.
# Reduce the result to combine partial sums.
result = partial_sums
num_shifts = int(log2(m) - log2(n))
shift = m // 2
for _ in range(num_shifts):
result += result.rotate(shift)
shift //= 2
# Mask out the first n entries
mask = [0] * m
for i in range(n):
mask[i] = 1
return result * Ciphertext(mask)
The squat and Halevi-Shoup functions could be easily combined,
with the last two blocks in the multiplication routine guarded by if n < m.
The squat method beats Halevi-Shoup in that it reduces the number of ciphertexts required to operate, which in turn reduces the number of rotations of the input. Even though this reduces opportunities to “hoist” rotations and adds additional rotations via the extra rotate-and-reduce step, it is more efficient overall when $n$ is much smaller than $m$, because the additional rotations required are logarithmic in $n$, while the savings in input rotations is $m - n >= n$ as $m >= 2n$. The alternative, in a naive sense, would be to pad the matrix with rows of zeros to make it square.
Next time
Next time I’d like to cover more advanced packing techniques, still just for matrix-vector multiplication. There are also packing techniques for convolution and more of the types of operations you’d see in a neural network. Moreover, there are techniques for converting between packings, as well as techniques for optimizing for the best packing choices across an entire program.
I don’t see how this is related to systolic arrays, which as far as I understand compute the sums and products more incrementally. If you know how, please tell me. ↩︎
Really, it requires the smaller dimension divide the larger dimension. But in our case, the cryptography requires the larger dimension to be a power of two. ↩︎
There may be more exotic methods to switch ciphertext dimension during the computation, but I’m not aware of them. ↩︎
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.