In my recent overview of homomorphic encryption, I underemphasized the importance of data layout when working with arithmetic (SIMD-style) homomorphic encryption schemes. In the FHE world, the name given to data layout strategies is called “packing,” because it revolves around putting multiple plaintext data into RLWE ciphertexts in carefully-chosen ways that mesh well with the operations you’d like to perform. By “mesh well” I mean it reduces the number of extra multiplications and rotations required merely to align data elements properly, rather than doing the actual computation you care about. Packing is an advanced topic, but it’s critical for performance and close to the cutting edge of FHE research.

Among this topic lie three sort of sub-problems:

This article is about the second problem: how do you convert between packings?

To start, we need to provide a rough interface for the computational model.

The Computational Model

The SIMD-style FHE computational model is loosely summarized as follows.

To go along with this, I implemented a simple Python object that represents the computational model. Rather than realistically implement an FHE scheme, it merely limits the API to the allowed operations. Borrowing from my packing strategies article, the file computational_model.py contains a class that limits the API to the allowed operations, ignoring limitations on bit precision for clarity.

class Ciphertext:
    def __init__(self, data: list[int]):
        self.data = data[:]
        self.dim = len(data)

    def __add__(self, other: "Ciphertext") -> "Ciphertext":
        assert self.dim == other.dim
        return Ciphertext([self.data[i] + other.data[i] for i in range(len(self.data))])

    def __mul__(self, other) -> "Ciphertext":
        if isinstance(other, Ciphertext):
            assert self.dim == other.dim
            return Ciphertext([self.data[i] * other.data[i] for i in range(len(self.data))])
        elif isinstance(other, list):
            # Plaintext-ciphertext multiplication
            assert self.dim == len(other) and isinstance(other[0], int)
            return Ciphertext([x * y for (x, y) in zip(self.data, other)])
        elif isinstance(other, int):
            # Plaintext-ciphertext multiplication
            return Ciphertext([other * x for x in self.data])

    def rotate(self, n: int) -> "Ciphertext":
        n = n % self.dim
        return Ciphertext(self.data[-n:] + self.data[:-n])

    ... (other helpers) ...

The essential problem behind packing conversion is that once data is laid out in an encrypted ciphertext, there is no elementary “shuffle” operation to permute data around. So if you want to do an elementwise addition or multiplication, and your inputs aren’t aligned properly, you have to use rotations, multiplications, and additions to align them, and these operations have nontrivial costs.

The problem statement

Given an integer-valued vector $v$ of length $N$, and a permutation $\sigma \in S_n$, construct a new vector $w$ with $w_i = v_{\sigma(i)}$ using only the following operations:

And do this in such a way that minimizes some explicit cost function of the generated circuit of operations.

In the paper Algorithms in HElib by Shai Halevi and Victor Shoup, they call this problem the Cheapest Shift Network problem and speculate it is hard.1

I still don’t quite understand what the right cost function should be. My initial guesses include:

The naive method

The naive method, which doesn’t seem so bad to me in many cases, is to split the permutation up into sets of common rotations.

That is, map each $i \mapsto s_i = \sigma(i) - i$ as the amount you need to rotate to get the $i$th element to its correct position. The preimage of a given $s_i$ is the set of all indices that can participate in the same rotation, so call it a rotation group.

Then, you can use multiplication-by-constants to apply a “bit mask” to the indices of each rotation group, rotate each group by its shift amount, and then add together all the results.

In code:

from collections import defaultdict
from computational_model import Ciphertext


def create_mask(indices: set[int], n: int) -> list[int]:
    """Create a mask of length n with 1s at the indices specified."""
    return [1 if i in indices else 0 for i in range(n)]


def mask_and_rotate(input: Ciphertext, permutation: dict[int, int]) -> Ciphertext:
    """Naively permutate the data entries in an FHE ciphertext."""
    # maps a shift to the indices that should be rotated by that amount
    rotation_groups = defaultdict(set)
    for i, sigma_i in permutation.items():
        rotation_groups[sigma_i - i].add(i)

    result = Ciphertext([0] * len(input))
    for shift, indices in rotation_groups.items():
        mask = create_mask(indices, len(input))
        result += (input * mask).rotate(shift)

    return result

In the worst case, the naive approach can require a number of rotation groups linear in the size of the input vector. The suboptimality in the worst case is a bit obvious: it’s easy to cook up an example where one element needs to be shifted by 3, another by 2, and a third by 1, and the element that is shifted by 3 can piggy back on the rotation groups for 1 and 2.

It seems like there should be a mechanism to build up rotations by reusing rotations by powers of 2. For some cost models, this would be great because it would trade off a small increase in the depth of the shift network for a exponential reduction in the number of rotation groups (linear to logarithmic).

The paper Algorithms in HElib does this using a technique called Benes networks. I initially wanted to implement this myself, but I found the explanations rather confusing and didn’t get over the hump of understanding it. It also seemed that their implementation was somewhat linear; each rotation only depended on the previous rotation, rather than building up a larger network of reusable rotations. So instead, I found a more recent paper that claims to improve on it, and I implemented that.

Vos-Vos-Erkin’s graph-coloring approach

The paper Efficient Circuits for Permuting and Mapping Packed Values Across Leveled Homomorphic Ciphertexts, by Jelle Vos, Daniël Vos, and Zekeriya Erkin, defines a method by splitting each desired rotation into a composition of rotations by powers of two corresponding to the binary representation of the desired rotation. I.e., a rotation by $5 = 101_2$ is a rotation by 1 and then by 4. All indices whose least-significant-bit is set are rotated by 1 at the same time, and so on for rotation by 2, 4, 8, etc. Each index participates in as many rotation groups as they have bits set.

However, this approach breaks when two elements would be rotated to the same intermediate position. For example, you might rotate index 3 by 5 positions to index 8, first rotating it by 1 to position 4, then rotating by 4 to position 8. If you must also rotate from index 4 to index 12 (a rotation by 4 then by 8), the rotation by 4 would also land it at index 8 at the same time as index 3 is being rotated there. Since, as in the naive method, the masked and rotated vectors are added together (with zeros expected in the unused positions), this would result in two elements being incorrectly added together.

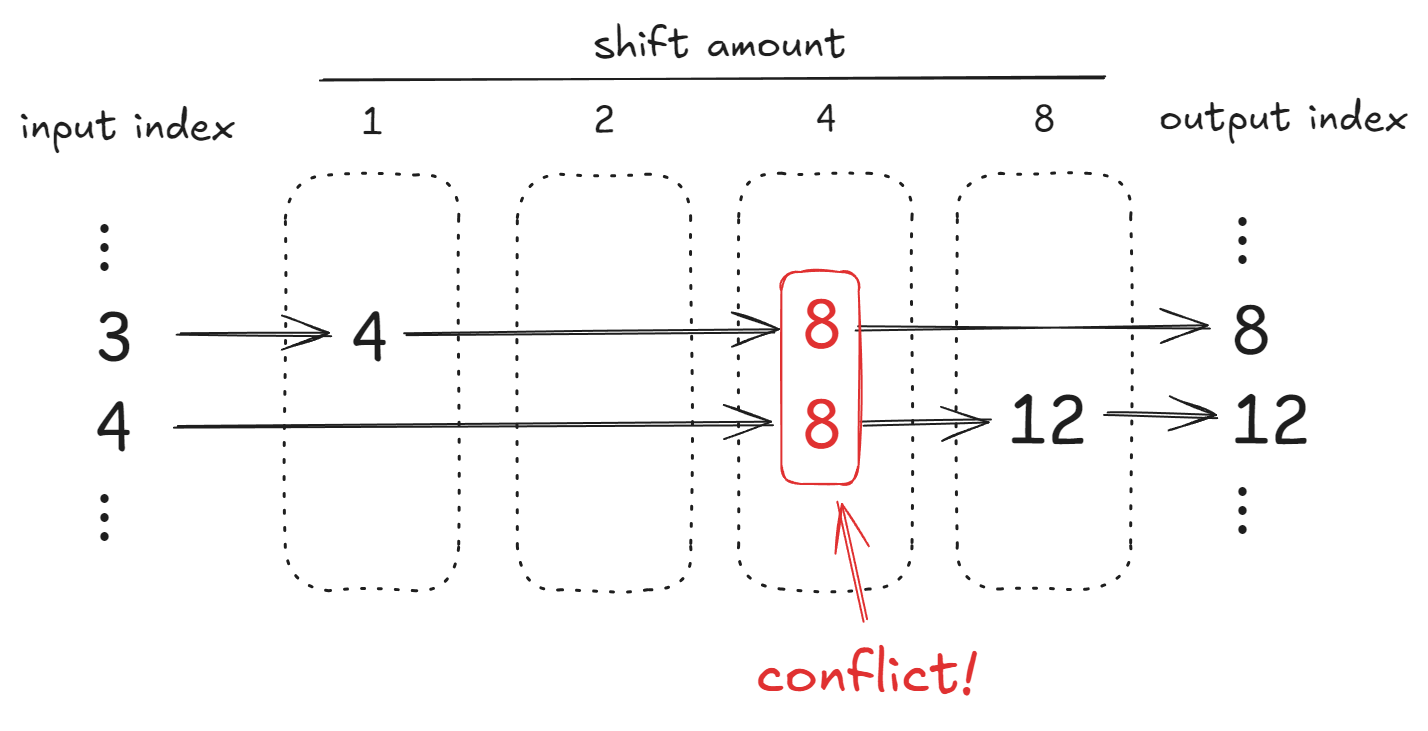
An example of a conflict when naively decomposing rotations

The paper identifies two ways to resolve this problem. First, you could pick a different ordering of the power-of-two rotations that happens to avoid collisions. In the example above, rotating by 4 first, or by 8 first, would avoid the collision. However, that could introduce other conflicts, and some conflicts may be unavoidable. So the second idea is to make separate sets of rotations to avoid collisions. In the example above, you’d have two different rotations by 4 instead of trying to rotate both indices in a single rotation.

The collisions comprise a natural graph coloring problem. Fix an ordering of the power-of-two rotations you plan to perform. Define a graph $G_\sigma$ whose vertices are the indices of the input vector, and whose edges are pairs of indices that would collide for the permutation $\sigma$ when decomposing and rotating according to the algorithm given above.

Then you color the graph with as few colors as possible. Each color corresponds to a full set of power-of-two rotations, and the indices assigned to color $c$ all participate in the same rotation groups for the corresponding set of power-of-two rotations.

In code, the implementation involves reconstructing a general version of the table in the figure above,

import itertools
from dataclasses import dataclass
import networkx as nx


@dataclass(frozen=True)
class RotationGroup:
    """A group of input vector indices that can safely be decomposed into
       power-of-two shifts and rotated without conflicts."""
    indices: frozenset[int]


def vos_vos_erkin(n: int, permutation: dict[int, int]) -> list[RotationGroup]:
    """Partition the input indices into groups that can be safely decomposed
       and rotated together."""
    assert set(permutation.keys()) == set(range(n))

    shifts = [(permutation[i] - i) % n for i in range(n)]
    format_string = f"{{:0{n.bit_length() - 1}b}}"

    # LSB-to-MSB ordering of bits of each shift
    shift_bits = [
        [int(b) for b in reversed(format_string.format(shift))] for shift in shifts
    ]

    # Here we compute the coresponding table of values after each rotation,
    # used to identify conflicts that would occur if the rotations were
    # performed naively.
    rounds = []
    for i in range(n.bit_length() - 1):
        rotation_amount = 1 << i
        last_round = rounds[-1] if rounds else {x: x for x in range(n)}
        rounds.append(
            {
                x: (last_round[x] + rotation_amount if bits[i] == 1 else x)
                for (x, bits) in zip(range(n), shift_bits)
            }
        )

    # Any two keys with colliding values in a round require an edge in G.
    G = nx.Graph()
    for round in rounds:
        for x, y in itertools.combinations(round.keys(), 2):
            if round[x] == round[y]:
                G.add_edge(x, y)

    coloring = nx.coloring.greedy_color(G, strategy="saturation_largest_first")

    indices_by_color = [[] for _ in range(1 + max(coloring.values()))]
    for index, color in coloring.items():
        indices_by_color[color].append(index)

    return [
        RotationGroup(indices=frozenset(group)) for group in indices_by_color
    ]

We use networkx to compute the graph coloring, which uses a greedy heuristic called DSatur which orders the vectices by “degree of saturation.” The method is not particularly important, and any decent coloring algorithm will do.

Note the code above does not convert the colored graph into a circuit of rotations, it just identifies a good partition, and then each partition would be decomposed into powers of two, and the mask_and_rotate function from the naive method could be used based on which bits are set.

Additional notes on Vos-Vos-Erkin

The paper had some additional heuristics and notes on what could be done to improve on their method:

Musing on other approaches to the Cheapest Shift Network problem

One nice thing about the cheapest shift network problem is that I want to implement solutions in our FHE compiler, HEIR. And since FHE programs are relatively small, and only need to be compiled once before being run many times, the tolerance for slow compilation time to get better programs is much higher than a traditional compiler.

So while this problem as a few nice heuristic solutions, I’d be interested to try something more heavyweight. I tinkered around with integer linear program (ILP) and contraint programming (CP-SAT) formulations, but I didn’t get very far. Part of what’s difficult is that this feels like circuit synthesis in the sense that the network structure is not fixed in advance, which makes it harder to encode as an ILP. The vectorization aspect of this problem also makes it seem like there’s not much other literature I can find that directly applies. For example, most literature on vectorizing programs is about converting loops to small-length vectorized operations, while we have essentially a straight-line program with large vector sizes (dimension 4096 - 65536) and a very limited set of operations.

I’m not as familiar with the actual methods people use for circuit synthesis, so I’d love to hear from you if you think you’ve got a hammer that fits this nail. Or if you know of any NP-complete problems this seems similar to, maybe we can prove it’s hard, though that wouldn’t help me and my compiler buddies.

  1. It is obviously in NP, but not clear if it is NP-hard. Though the Halevi-Shoup paper was written in 2014 (ten years from the publication of this article), I’m not aware of any more recent results establishing it as NP-hard. The authors of the 2022 Vos-Vos-Erkin paper mentioned later in this article also seem to think its complexity is not known. It seems to be analogous to a vectorized and arithmetic variant of minimum circuit size problem (MCSP), though MCSP also has unknown complexity: it’s in NP but not known to be NP-complete, see the intro to this paper for more info. ↩︎

Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.

DOI: https://doi.org/10.59350/wf2m2-8vs89