There’s a family of tabletop games that are based directly on a nontrivial mathematics problem. As a casual and fun way to inaugurate my new blog (migrated from Wordpress to Hugo, after my work on getting better LaTeX mathmode support in Hugo), I thought I’d write a short listicle about them, so that I have a place to add more as I find them, as well as give the shortest canonical description of the associated math problem.
This isn’t a place for games whose core mechanic is explicit mental arithmetic like 24, nor games whose explicit purpose is to teach math concepts in a fun way, like Prime Climb, nor games that “merely” promote logical thinking in some abstract sense, like Chess or Go. Rather, my goal is to list games that are both fun for adults to play (and likely children), don’t necessarily require learning any mathematics to enjoy, but are based on some deeper mathematical structure or concept that could be explored if desired.
SET

The game of SET
The most famous game in this category, the goal of SET is to find sets of three cards for which each of the four attributes (color, shape, number, and fill) has either the same value across all three cards or unique values across all three cards. Players race to find sets, and deal out more cards each time a set is found. Discussed more here and here (pdf link).
The math problem: Given a set of points in the vector space $\mathbb{F}_3^4$ (4-tuples of integers mod 3), determine if any three points form a line.
Followup: how many cards are necessary to deal to ensure a set exists? What is the maximum size of a point set in $\mathbb{F}_3^4$ such that no three points are collinear? What about larger spaces $\mathbb{F}_p^k$?
Spot it!
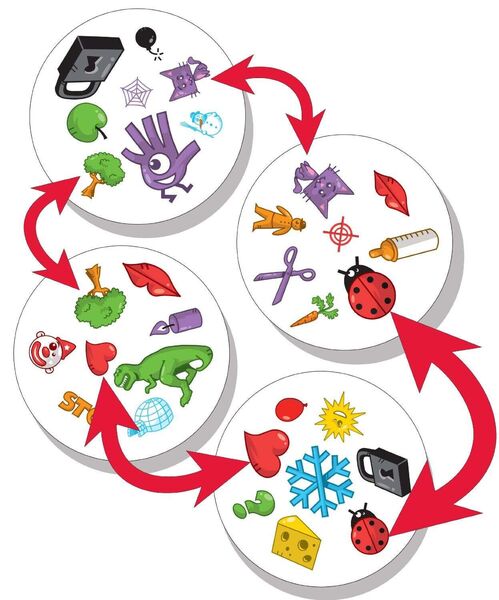
The game Spot It!
Spot It!, also known as Dobble, is a matching game where players race to identify a common image between two cards that contain a variety of images of different sizes and orientations. It is guaranteed that any two cards has exactly one image in common. Discussed in more detail here and here.
The math problem: Given two lines in the finite projective plane of order 7 (a set system with 57 points, 57 lines, 8 points per line, and 8 lines passing through each point), identify the unique point of their intersection.
Followup: how does one construct a finite projective plane of a given order? What point set sizes are possible?
Hanabi

The game of Hanabi
Hanabi is a cooperative twist on Solitaire where players can see everyone’s cards but their own, and take turns either playing a card from their hand or giving a restricted piece of information to another player (they indicate all cards of a certain number or color in other player’s hand). Discussed more here and here.
The math problem: Given a set of people wearing red/blue hats, each of whom can see everyone else’s hat color but not their own, give one bit of information that tells everyone else the color of their own hat.
(Okay, Hanabi is less directly related to the hat coloring puzzles than the other games in this list are to their math problems, but I like Hanabi and wanted to include it.)
Followup: red/blue hat puzzles and more infinite hat puzzles.
Socks

The game of Socks
(Disclaimer: I sell a version of this game here)
In Socks, the goal is to find a subset of the dealt cards for which all socks in the subset can be matched up in matching pairs. I.e., each type of sock in the subset must appear an even number of times. Discussed more here.
The math problem: Given a subset of $(\mathbb{Z}/2\mathbb{Z})^6$ (6-tuples of integers mod 2), find a zero-summing subset.
Followup: How many cards are necessary to guarantee a zero-summing subset? What is the required size to ensure a zero-summing subset of $(\mathbb{Z}/2\mathbb{Z})^k$? Of $(\mathbb{Z}/n\mathbb{Z})^k$? This value is called Olson’s constant.
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.