Before I discovered math, I was a first year undergrad computer science student taking Electrical Engineering 101. The first topic I learned was what bits and boolean gates are, and the second was the two’s complement representation of a negative n-bit integer.
At the time two’s complement seemed to me like a bizarre quirk of computer programming, with minutiae you just had to memorize. If the leading bit is 1, it’s negative, and otherwise it’s positive. To negate a number, flip the bits and add one. Except of course the number 1000 0000, which in 8-bit two’s complement is -128, because its “negative” according to this operation is also 1000 0000 = -128.
The quirky negation operation is usually explained by appealing to the “borrowing” operation from elementary school subtraction. Or an appeal to a sense of shared helplessness. That’s just the way things are in two’s complement. But it doesn’t quite explain why one can use the same boolean circuit to compute addition and multiplication of unsigned and two’s complement signed integers.
Math can provide a different, clearer explanation for the quirkiness. It’s not arbitrary, but forced. The explanation uses group theory, which I wrote a primer about a long time ago. The main ideas from group theory used here are cyclic groups, quotient groups, group isomorphisms, and group actions.
The first insight is that the signed integers are the exact same as the unsigned integers as a quotient group, just with a different equivalence class representative chosen for the arithmetic.
The set of $n$-bit unsigned integers $\mathbb{Z}/2^n\mathbb{Z} = \{ 0, 1, \dots, 2^n-1 \}$ forms a group under addition modulo $2^n$. The set of $n$-bit signed integers $\{ -2^{n-1}, \dots, -1, 0, 1, \dots, 2^{n-1} – 1 \}$ also forms a group, but it’s harder to see why. The operation is still “addition modulo $2^n$”, but you have to recall the definition of a quotient group to see why.
The elements of the quotient group $\mathbb{Z}/2^n \mathbb{Z}$ aren’t integers, but rather equivalence classes of integers. We denote $[x] \in \mathbb{Z}/2^n \mathbb{Z}$ as the equivalence class of $x \in \mathbb{Z}$. For example, the “element” $1$ is the equivalence class $[1] = \{ \dots, -2^n+1, 1, 2^n + 1, 2\cdot 2^n + 1, \dots \}$. And the whole point of defining equivalence classes is that you can choose any representative element from an equivalence class, do the arithmetic using that element, and you get the same (equivalence class) output as you would if you had used the “usual” representative. In other words, it’s guaranteed that $[x+y] = [x] + [y] = [x’] + [y’] = [x’ + y’]$, so long as $[x] = [x’]$ and $[y] = [y’]$.
Signed integers are exactly this: choosing a different representative for some of the equivalence classes. The element $[2^{n-1}] = \{ \dots, -2\cdot 2^{n-1}, -2^{n-1}, 2^{n-1}, 2\cdot 2^{n-1}, \dots \}$ is represented by $-2^{n-1}$, the element $[2^{n-1} + 1]$ is represented by $-2^{n-1} + 1$, all the way up to $2^n – 1$ being represented by $-1$. This is a formal way to say two’s complement is a “reinterpretation” of the bits of an unsigned integer. It’s not an arbitrary reinterpretation, but one that satisfies the exact same arithmetic structure as the unsigned interpretation.
So any circuit representation of an addition operation that works for unsigned integers can also be used for addition for all possible alternative choices of equivalence class representatives. Note this has nothing to do with the way these numbers are represented as bits. It’s a guarantee of the mathematics underlying modular arithmetic. It would work if the numbers were represented in ternary or base 10 (excluding the fact that there would be some extra inputs and outputs not in the set). Also note it applies equally well to multiplication, since everything said here applies equally well to the quotient ring of integers modulo $2^n$.
It also makes it clear that the choice of $-2^{n-1}$ as the smallest negative number is arbitrary, and one could equally well include $2^n-1$ as the largest positive, leaving $-2^{n-1} + 1$ as the smallest negative. I think the current standard choice ($-2^{n-1}$ as the smallest negative number) is objectively better than this alternative, because it allows one to use the leading sign bit as negativeness/overflow/underflow detector.
Now we can study the negation operation in this group. For starters, for each element $x$ except $-2^{n-1}$, the number $-x$ is already a signed $n$-bit integer. So negation is just negation (we’ll get back to how this is interpreted as bits in a second). And if we think of $-2^{n-1}$ as an equivalence class, it’s the same as $2^{n-1}$, which is its own inverse as an unsigned integer. Add it to itself and you get $2^n \equiv 0 \mod 2^n$. Since equivalence classes behave identically no matter the representative, $-2^{n-1}$ must be its own inverse, and hence $-(-2^{n-1}) = -2^{n-1}$ as signed integers.
To interpret it as bits, again lift back to unsigned integers, and notice that “negation” for an unsigned integer $x$—that is, finding the value $y$ such that $x+y \equiv 0 \mod 2^n$—is computed via $-[x] = [2^n – x]$ (subtraction inside the equivalence class is defined even though it’s being used to define $-[x]$, because inside an equivalence class the arithmetic is just arithmetic on integers). But because $2^n$ isn’t representable in concrete $n$-bit numbers (it’s just zero), to compute it entirely within $n$-bit integers, we need to break the arithmetic down further:
$$ [2^n – x ] = [ 2^n – 1 – x + 1 ] = [ 2^n – 1 – x ] + [ 1 ] $$$2^n-1$ is the string of all 1’s, hence $2^n – 1 – x$ is equivalent to flipping the bits of $x$, and adding 1 finishes the calculation.
Finally, this $-2^{n-1}$-is-its-own-inverse business. If you view the group of unsigned integers as a circle—a natural choice because addition “wraps around” like clock math—the negation operation can be seen as a reflection across the line passing through $0$ and the circle’s center. Naturally this makes the negation of $0$ equal to $0$. The other point that line of symmetry passes through is $[2^{n-1}] = [-2^{n-1}]$, and so it must also fix $-2^{n-1}$.
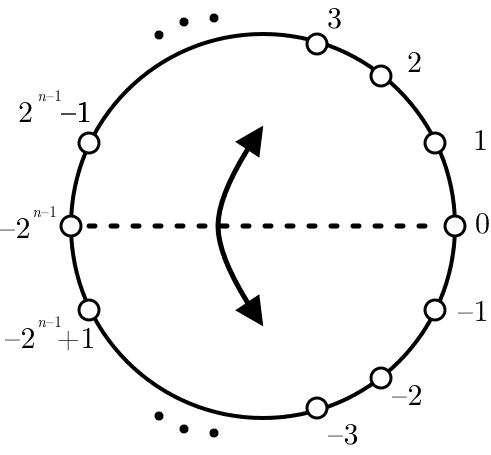
Signed $n$-bit integers visualized on a circle. Reflection across the dashed horizontal line defines negation.
This is explanation enough, but the pesky question is whether it’s forced. Is there some other representation better than two’s complement for which this behavior doesn’t occur? So long as our number system has an even size and 0 is its own inverse, then simple counting shows it’s impossible. We’d have an odd number $2^n – 1$ of nonzero elements, and the inverse operation would match them up in pairs, producing an even total unless one of the “pairs” is a singleton.
Aside: The Wikipedia article on this topic had a somewhat sloppy explanation using group actions (really, Burnside’s lemma), which, while correct, is like using the Millennium Falcon to shoot a sparrow. I simplified it to the above counting argument.
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.