Our hero, a mathematician, is writing notes in LaTeX and needs to convert it to a format that her blog platform accepts. She’s used to using dollar sign delimiters for math mode, but her blog requires \( \) and \[ \]. Find-and-replace fails because it doesn’t know about which dollar sign is the start and which is the end. She knows there’s some computer stuff out there that could help, but she doesn’t have the damn time to sort through it all. Paper deadlines, argh!
If you want to skip ahead to a working solution, and you can run basic python scripts, see the Github repository for this post with details on how to run it and what the output looks like. It’s about 30 lines of code, and maybe 10 of those lines are not obvious. Alternatively, copy/paste the code posted inline in the section “First attempt: regular expressions.”
In this post I’ll guide our hero through the world of text manipulation, explain the options for solving a problem like this, and finally explain how to build the program in the repository from scratch. This article assumes you have access to a machine that has basic programming tools pre-installed on it, such as python and perl.
The problem with LaTeX
LaTeX is great, don’t get me wrong, but people who don’t have experience writing computer programs that operate on human input tend to write sloppy LaTeX. They don’t anticipate that they might need to programmatically modify the file because the need was never there before. The fact that many LaTeX compilers are relatively forgiving with syntax errors exacerbates the issue.
The most common way to enter math mode is with dollar signs, as in
Now let $\varepsilon > 0$ and set $\delta = 1/\varepsilon$.
For math equations that must be offset, one often first learns to use double-dollar-signs, as in
First we claim that $$0 \to a \to b \to c \to 0$$ is a short exact sequence
The specific details that make it hard to find and convert from this delimiter type to another are:
- Math mode can be broken across lines, but need not be.
- A simple search and replace for
$would conflict with$$. - The fact that the start and end are symmetric means a simple search and replace for
$$fails: you can’t tell whether to replace it with\[or\]without knowing the context of where it occurs in the document. - You can insert a dollar sign in LaTeX using
$and it will not enter math mode. (I do not solve this problem in my program, but leave it as an exercise to the reader to modify each solution to support this)
First attempt: regular expressions
The first thing most programmers will tell you when you have a text manipulation problem is to use regular expressions (or regex). Regular expressions are text patterns that a program called a regular expression engine uses to find subsets of text in a document. This can often be with the goal of modifying the matched text somehow, but also just to find places where the text occurs to generate a report.
In their basic form, regular expressions are based on a very clean theory called regular languages, which is a kind of grammar equivalent to “structure that can be recognized by a finite state machine.”
[Aside: some folks prefer to distinguish between regular expressions as implemented by software systems (regex) and regular expressions as a representation of a regular language; as it turns out, features added to regex engines make them strictly stronger than what can be represented by the theory of regular languages. In this post I will use “regex” and “regular expressions” both for practical implementations, because programmers and software don’t talk about the theory, and use “regular languages” for the CS theory concept]
The problem is that practical regular expressions are difficult and nit-picky, especially when there are exceptional cases to consider. Even matching something like a date can require a finnicky expression that’s hard for humans to read and debug when they are incorrect. A regular expression for a line in a file that contains a date by itself:
^\s*(19|20)\d\d[- /.](0[1-9]|1[012])[- /.](0[1-9]|[12][0-9]|3[01])\s*$
Worse, regular expressions are rife with “gotchas” having to do with escape characters. For example, parentheses are used for something called “capturing”, so you have to use ( to insert a literal parenthesis. If having to use “$” in LaTeX bothers you, you’ll hate regular expressions.
Another issue comes from history. There was a time when computers only allowed you to edit a file one line at a time. Many programming tools and frameworks were invented during this time that continue to be used today (you may have heard of sed which is a popular regular expression find/replace program—one I use almost daily). These tools struggle to operate on problems that span many lines of a file, because they simply weren’t designed for that. Problem (1) above suggests this might be a problem.
Yet another issue is in slight discrepancies between regex engines. Perl, python, sed, etc., all have slight variations and “nonstandard” features. As all programmers know, every visible behavior of a system will eventually be depended on by some other system.
But the real core problem is that regular expressions weren’t really designed for knowing about the context where a match occurs. Regular expressions are designed to be character-at-a-time pattern matching. [edit: removed an incorrect example] But over time, regular expression engines have added features to do such things over the years (which makes them more powerful than the original, formal definition of a regular language, and even more powerful than what parsers can handle!), but the more complicated you make a regular expression, the more likely it’s going to misbehave on odd inputs, and less likely others can use it without bugs or modification for their particular use case. Software engineers care very much about such things, though mathematicians needing a one-off solution may not.
One redeeming feature of regular expressions is that—by virtue of being so widely used in industry—there are many tools to work with them. Every major programming language has a regular expression engine built in. And many websites help explain how regexes work. regexr.com is one I like to use. Here is an example of using that website to replace offset mathmode delimiters. Note the “Explain” button, which traces the regex engine as it looks for matches.
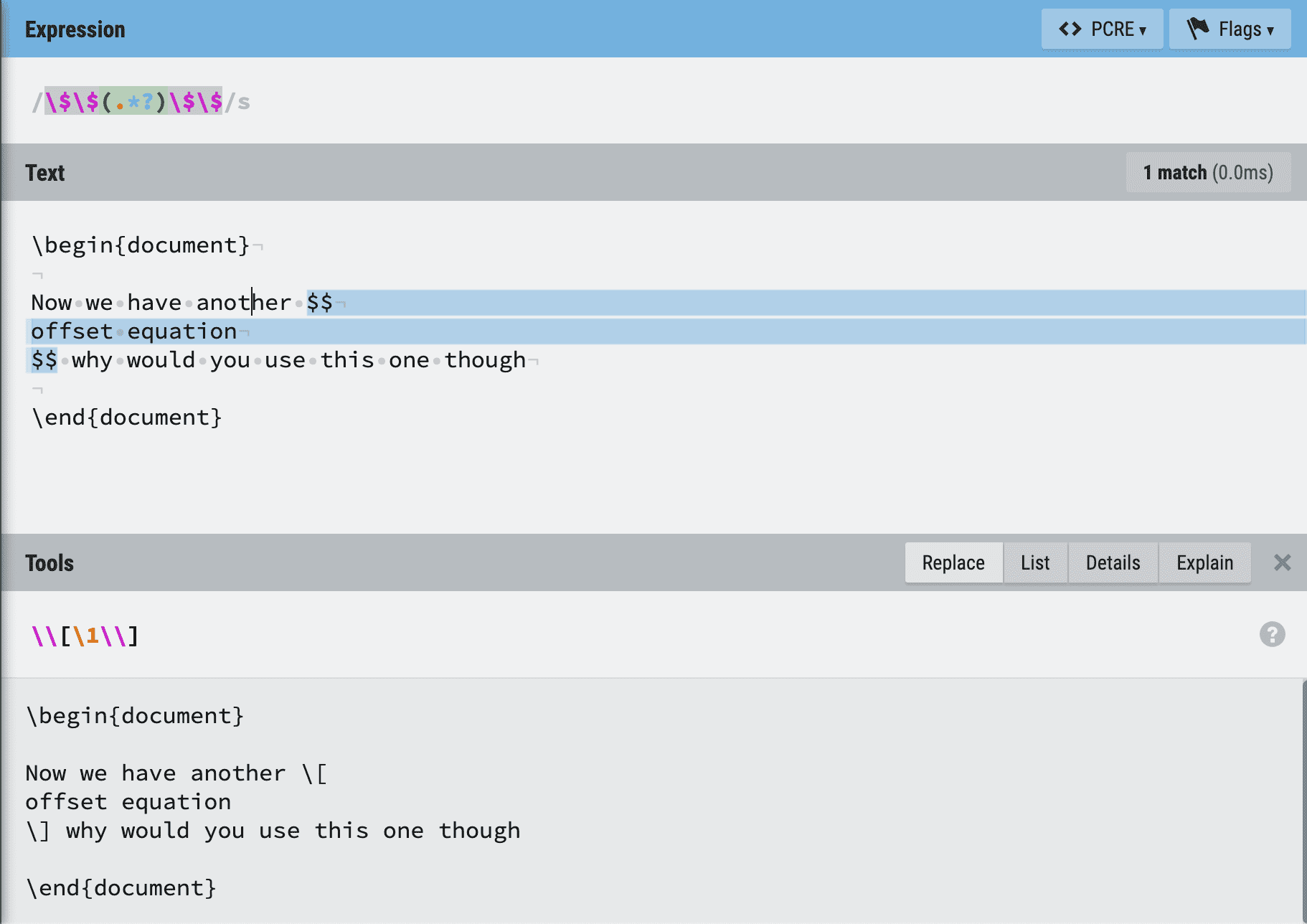
So applying this to our problem: we can use two regular expressions to solve the problem. I’m using the perl programming language because its regex engine supports multiline matches. All MacOS and linux systems come with perl pre-installed.
perl -0777 -pe 's/\$\$(.*?)\$\$/\\[\1\\]/gs' < test.tex \
| perl -0777 -pe 's/\$(.*?)\$/\\(\1\\)/gs' > output.tex
Now let’s explain, starting with the core expressions being matched and replaced.
s/X/Y/ tells a regex engine to “substitute regex matches of X with Y”. In the first regex X is \$\$(.*?)\$\$, which breaks down as:
\$\$match two literal dollar signs(capture a group of characters signified by the regex between here and the matching closing parenthesis.*zero or more of any character?looking at the “zero or more” in the previous step, try to match as few possible characters as you can while still making this pattern successfully match something
)stop the capture group, and save it as group1\$\$match two more literal dollar signs
Then Y is the chosen replacement. We’re processing offset mathmode, so we want [ ]. Y is [\1], which means
\\a literal backslash[a literal open bracket\1the first capture group from the matched expression\\a literal backslash]a literal close bracket
All together we have s/\$\$(.*?)\$\$/\\[\1\\]/, but then we add a final s and g characters, which act as configuration. The s tells the regex engine to allow the dot . to match newlines (so a pattern can span multiple lines) and the g tells the regex to apply the substitution globally to every match it sees—as opposed to just the first.
Finally, the full first command is
perl -0777 -pe 's/\$\$(.*?)\$\$/\\[\1\\]/gs' < test.tex
This tells perl to read in the entire test.tex file and apply the regex to it. Broken down:
perlrun perl-0777read the entire file into one string. If you omit it, perl will apply the regex to each line separately.-pwill make perl automatically “read input and print output” without having to tell it to with a “print” statementetells perl to run the following command line argument as a program.< test.textells perl to use the file test.tex as input to the program (as input to the regex engine, in this case).
Then we pipe the output of this first perl command to a second one that does a very similar replacement for inline math mode.
<first_perl_command> | perl -0777 -pe 's/\$(.*?)\$/\\(\1\\)/gs'
The vertical bar | tells the shell executing the commands to take the output of the first program and feed it as input to the second program, allowing us to chain together sequences of programs. The second command does the same thing as the first, but replacing $ with \( and \). Note, it was crucial we had this second program occur after the offset mathmode regex, since $ would match $$.
Exercise: Adapt this solution to support Problem (4), support for literal \$ dollar signs. Hint: you can either try to upgrade the regular expression to not be tricked into thinking \$ is a delimiter, or you can add extra programs before that prevent \$ from being a problem. Warning: this exercise may cause a fit.
It can feel like a herculean accomplishment to successfully apply regular expressions to a problem. You can appreciate the now-classic programmer joke from the webcomic xkcd:

Regular Expressions
However, as you can tell, getting regular expressions right is hard and takes practice. It’s great when someone else solves your problem exactly, and you can copy/paste for a one-time fix. But debugging regular expressions that don’t quite work can be excruciating. There is another way!
Second attempt: using a parser generator
While regular expressions have a clean theory of “character by character stateless processing”, they are limited. It’s not possible to express the concept of “memory” in a regular expression, and the simplest example of this is the problem of counting. Suppose you want to find strings that constitute valid, balanced parentheticals. E.g., this is balanced:
(hello (()there)() wat)
But this is not
(hello ((there )() wat)
This is impossible for regexes to handle because counting the opening parentheses is required to match the closing parens, and regexes can’t count arbitrarily high. If you want to parse and manipulate structures like this, that have balance and nesting, regex will only bring you heartache.
The next level up from regular expressions and regular languages are the two equivalent theories of context-free grammars and pushdown automata. A pushdown automaton is literally a regular expression (a finite state machine) equipped with a simple kind of memory called a stack. Rather than dwell on the mechanics, we’ll see how context-free grammars work, since if you can express your document as a context free grammar, a tool called a parser generator will give you a parsing program for free. Then a few simple lines of code allow you to manipulate the parsed representation, and produce the output document.
The standard (abstract) notation of a context-free grammar is called Extended Backus-Naur Form (EBNF). It’s a “metasyntax”, i.e., a syntax for describing syntax. In EBNF, you describe rules and terminals. Terminals are sequences of constant patterns, like
OFFSET_DOLLAR_DELIMITER = $$
OFFSET_LEFT_DELIMITER = \[
OFFSET_LEFT_DELIMITER = \]
A rule is an “or” of sequences of other rules or terminals. It’s much easier to show an example:
char = "a" | "b" | "c"
offset = OFFSET_DOLLAR_DELIMITER char OFFSET_DOLLAR_DELIMITER
| OFFSET_LEFT char OFFSET_RIGHT
The above describes the structure of any string that looks like offset math mode, but with a single a or a single b or a single c inside, e.g, \[b\]. You can see some more complete examples on Wikipedia, though they use a slightly different notation.
With some help from a practical library’s built-in identifiers for things like “arbitrary text” we can build a grammar that covers all of the ways to do latex math mode.
latex = content
content = content mathmode content | TEXT | EMPTY
mathmode = OFFSETDOLLAR TEXT OFFSETDOLLAR
| OFFSETOPEN TEXT OFFSETCLOSE
| INLINEOPEN TEXT INLINECLOSE
| INLINE TEXT INLINE
INLINE = $
INLINEOPEN = \(
INLINECLOSE = \)
OFFSETDOLLAR = $$
OFFSETOPEN = \[
OFFSETCLOSE = \]
Here we’re taking advantage of the fact that we can’t nest mathmode inside of mathmode in LaTeX (you probably can, but I’ve never seen it), by defining the mathmode rule to contain only text, and not other instances of the content rule. This rules out some ambiguities, such as whether $x$ y $z$ is a nested mathmode or not.
We may not need the counting powers of context-free grammars, yet EBNF is easier to manage than regular expressions. You can apply context-sensitive rules to matches, whereas with regexes that would require coordination between separate passes. The order of operations is less sensitive; because the parser generator knows about all patterns you want to match in advance, it will match longer terminals before shorter—more ambiguous—terminals. And if we wanted to do operations on all four kinds of math mode, this allows us to do so without complicated chains of regular expressions.
The history of parsers is long and storied, and the theory of generating parsing programs from specifications like EBNF is basically considered a solved problem. However, there are a lot of parser generators out there. And, like regular expression engines, they each have their own flavor of EBNF—or, as is more popular nowadays, they have you write your EBNF using the features of the language the parser generator is written in. And finally, a downside of using a parser generator is that you have to then write a program to operate on the parsed representation (which also differs by implementation).
We’ll demonstrate this process by using a Python library that, in my opinion, stays pretty faithful to the EBNF heritage. It’s called lark and you can pip-install it as
pip install lark-parser
Note: the hard-core industry standard parser generators are antlr, lex, and yacc. I would not recommend them for small parsing jobs, but if you’re going to do this as part of a company, they are weighty, weathered, well-documented—unlike lark.
Lark is used entirely inside python, and you specify the EBNF-like grammar as a string. For example, ours is
tex: content+
?content: mathmode | text+
mathmode: OFFSETDOLLAR text+ OFFSETDOLLAR
| OFFSETOPEN text+ OFFSETCLOSE
| INLINEOPEN text+ INLINECLOSE
| INLINE text+ INLINE
INLINE: "$"
INLINEOPEN: "\\("
INLINECLOSE: "\\)"
OFFSETDOLLAR: "$$"
OFFSETOPEN: "\\["
OFFSETCLOSE: "\\]"
?text: /./s
You can see the similarities with our “raw” EBNF. The main difference here is the use of + for matching “one or more” of a rule, the use of a regular expression to define the “text” rule as any character (here again the trailing s means: allow the dot character to match newline characters). The backslashes are needed because backslash is an escape character in Python. And finally, the question mark tells lark to try to compress the tree if it only matches one item (you can see what the difference is by playing with our display-parsed-tree.py script that shows the parsed representation of the input document. You can read more in lark’s documentation about what the structure of the parsed tree is as python objects (Tree for rule/terminal matches and Token for individual characters).
For the input Let $x=0$, the parsed tree is as follows (note that the ? makes lark collapse the many “text” matches):
Tree(tex,
[Tree(content,
[Token(__ANON_0, 'L'),
Token(__ANON_0, 'e'),
Token(__ANON_0, 't'),
Token(__ANON_0, ' ')]),
Tree(mathmode,
[Token(INLINE, '$'),
Token(__ANON_0, 'x'),
Token(__ANON_0, '='),
Token(__ANON_0, '0'),
Token(INLINE, '$')]),
Token(__ANON_0, '\n')])
So now we can write a simple python program that traverses this tree and converts the delimiters. The entire program is on Github, but the core is
def join_tokens(tokens):
return ''.join(x.value for x in tokens)
def handle_mathmode(tree_node):
'''Switch on the different types of math mode, and convert
the delimiters to the desired output, and then concatenate the
text between.'''
starting_delimiter = tree_node.children[0].type
if starting_delimiter in ['INLINE', 'INLINEOPEN']:
return '\\(' + join_tokens(tree_node.children[1:-1]) + '\\)'
elif starting_delimiter in ['OFFSETDOLLAR', 'OFFSETOPEN']:
return '\\[' + join_tokens(tree_node.children[1:-1]) + '\\]'
else:
raise Exception("Unsupported mathmode type %s" % starting_delimiter)
def handle_content(tree_node):
'''Each child is a Token node whose text we'd like to concatenate
together.'''
return join_tokens(tree_node.children)
The rest of the program uses lark to create the parser, reads the file from standard input, processes the parsed representation, and outputs the converted document to standard output. You can use the program like this:
python convert-delimiters.py < input.tex > output.tex
Exercise: extend this grammar to support literal dollar signs using \$, and passes them through to the output document unchanged.
What’s better?
I personally prefer regular expressions when the job is quick. If my text manipulation rule fits on one line, or can be expressed without requiring “look ahead” or “look behind” rules, regex is a winner. It’s also a winner when I only expect it to fail in a few exceptional cases that can easily be detected and fixed by hand. It’s faster to write a scrappy regex, and then open the output in a text editor and manually fix one or two mishaps, than it is to write a parser.
However, the longer I spend on a regular expression problem—and the more frustrated I get wrestling with it—the more I start to think I should have used a parser all along. This is especially true when dealing with massive jobs. Such as converting delimiters in hundreds of blog articles, each thousands of words long, or making changes across all chapter files of a book.
When I need something in between rigid structure and quick-and-dirty, I actually turn to vim. Vim has this fantastic philosophy of “act, repeat, rewind” wherein you find an edit that applies to the thing you want to change, then you search for the next occurrence of the start, try to apply the change again, visually confirm it does the right thing, and if not go back and correct it manually. Learning vim is a major endeavor (for me it feels lifelong, as I’m always learning new things), but since I spend most of my working hours editing structured text the investment and philosophy has paid off.
Until next time!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.