Problem: Design a random number generator that is computationally indistinguishable from a truly random number generator.
Solution (in Python): note this solution uses the Miller-Rabin primality tester, though any primality test will do. See the github repository for the referenced implementation.
from randomized.primality import probablyPrime
import random
def goodPrime(p):
return p % 4 == 3 and probablyPrime(p, accuracy=100)
def findGoodPrime(numBits=512):
candidate = 1
while not goodPrime(candidate):
candidate = random.getrandbits(numBits)
return candidate
def makeModulus():
return findGoodPrime() * findGoodPrime()
def parity(n):
return sum(int(x) for x in bin(n)[2:]) % 2
class BlumBlumShub(object):
def __init__(self, seed=None):
self.modulus = makeModulus()
self.state = seed if seed is not None else random.randint(2, self.modulus - 1)
self.state = self.state % self.modulus
def seed(self, seed):
self.state = seed
def bitstream(self):
while True:
yield parity(self.state)
self.state = pow(self.state, 2, self.modulus)
def bits(self, n=20):
outputBits = ''
for bit in self.bitstream():
outputBits += str(bit)
if len(outputBits) == n:
break
return outputBits
Discussion:
An integer $ x$ is called a quadratic residue of another integer $ N$ if it can be written as $ x = a^2 \mod N$ for some $ a$. That is, if it’s the remainder when dividing a perfect square by $ N$. Some numbers, like $ N=8$, have very special patterns in their quadratic residues, only 0, 1, and 4 can occur as quadratic residues.
The core idea behind this random number generator is that, for a specially chosen modulus $ N$, telling whether a number $ x$ is a quadratic residue mod $ N$ is hard. In fact, one can directly convert an algorithm that can predict the next bit of this random number generator (by even a slight edge) into an arbitrarily accurate quadratic-residue-decider. So if computing quadratic residues is even mildly hard, then predicting the next bit in this random number generator is very hard.
More specifically, the conjectured guarantee about this random number generator is the following: if you present a polynomial time adversary with two sequences:
- A truly random sequence of bits of length $ k$,
- $ k$ bits from the output of the pseudorandom generator when seeded with a starting state shorter than $ k$ bits.
Then the adversary can’t distinguish between the two sequences with probability “significantly” more than 1/2, where by “significantly” I mean $ 1/k^c$ for any $ c>0$ (i.e., the edge over randomness vanishes faster than any inverse polynomial). It turns out, due to a theorem of Yao, that this is equivalent to not being able to guess the next bit in a pseudorandom sequence with a significant edge over a random guess, even when given the previous $ \log(N)^{10}$ bits in the sequence (or any $ \textup{poly}(\log N)$ bits in the sequence).
This emphasizes a deep philosophical viewpoint in theoretical computer science, that whether some object has a property (randomness) really only depends on the power of a computationally limited observer to identify that property. If nobody can tell the difference between fake randomness and real randomness, then the fake randomness is random. Offhand I wonder whether you can meaningfully apply this view to less mathematical concepts like happiness and status.
Anyway, the modulus $ N$ is chosen in such a way that every quadratic residue of $ N$ has a unique square root which is also a quadratic residue. This makes the squaring function a bijection on quadratic residues. In other words, with a suitably chosen $ N$, there’s no chance that we’ll end up with $ N=8$ where there are very few quadratic residues and the numbers output by the Blum-Blum-Shub generator have a short cycle. Moreover, the assumption that detecting quadratic residues mod $ N$ is hard makes the squaring function a one-way permutation.
Here’s an example of how this generator might be used:
generator = BlumBlumShub()
hist = [0] * 2**6
for i in range(10000):
value = int(generator.bits(6), 2)
hist[value] += 1
print(hist)
This produces random integers between 0 and 64, with the following histogram:
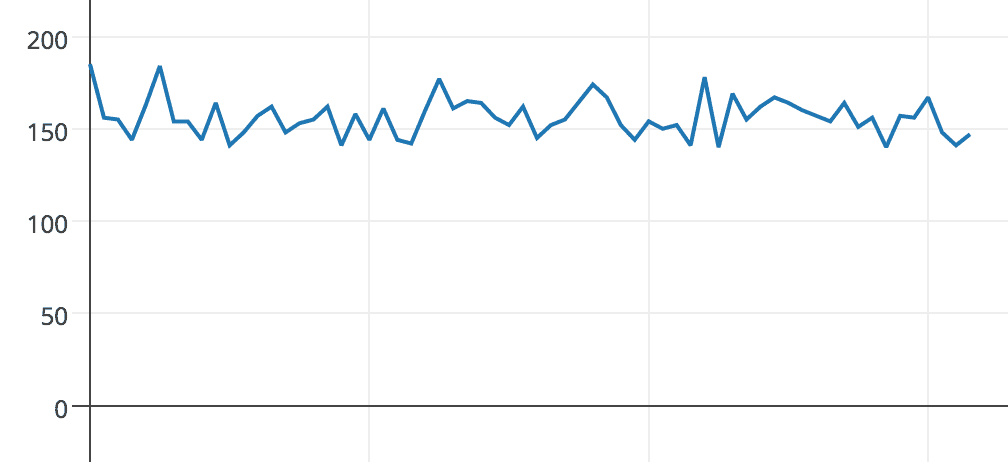
bbs-hist
See these notes of Junod for a detailed exposition of the number theory behind this random number generator, with full definitions and proofs.
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.