Last time we left off with a tantalizing conjecture: a random graph with edge probability $ p = 5/n$ is almost surely a connected graph. We arrived at that conjecture from some ad-hoc data analysis, so let’s go back and treat it with some more rigorous mathematical techniques. As we do, we’ll discover some very interesting “threshold theorems” that essentially say a random graph will either certainly have a property, or it will certainly not have it.
phase-transition-n-grows
Big components
Recalling the basic definition: an Erdős-Rényi (ER) random graph with $ n$ vertices and edge probability $ p$ is a probability distribution over all graphs on $ n$ vertices. Generatively, you draw from an ER distribution by flipping a $ p$-biased coin for each pair of vertices, and adding the edge if you flip heads. We call the random event of drawing a graph from this distribution a “random graph” even though it’s not a graph, and we denote an ER random graph by $ G(n,p)$. When $ p = 1/2$, the distribution $ G(n,1/2)$ is the uniform distribution over all graphs on $ n$ vertices.
Now let’s get to some theorems. The main tools we’ll use are called the first and second moment method. Let’s illustrate them by example.
The first moment method
Say we want to know what values of $ p$ are likely to produce graphs with isolated vertices (vertices with no neighbors), and which are not. Of course, the value of $ p$ will depend on $ n \to \infty$ in general, but we can already see by example that if $ p = 1/2$ then the probability of a fixed vertex being isolated is $ 2^{-n} \to 0$. We can use the union bound (sum this value over all vertices) to show that the probability of any vertex being isolated is at most $ n2^{-n}$ which also tends to zero very quickly. This is not the first moment method, I’m just making the point that all of our results will be interpreted asymptotically as $ n \to \infty$.
So now we can ask: what is the expected number of isolated vertices? If I call $ X$ the random variable that counts the expected number of isolated vertices, then I’m asking about $ \mathbb{E}[X]$. Really what I’m doing is interpreting $ X$ as a random variable depending on $ n, p(n)$, and asking about the evolution of $ \mathbb{E}[X]$ as $ n \to \infty$.
Now the first moment method states, somewhat obviously, that if the expectation tends to zero then the value of $ X$ itself also tends to zero. Indeed, this follows from Markov’s inequality, which states that the probability that $ X \geq a$ is bounded by $ \mathbb{E}[X]/a$. In symbols,
$ \displaystyle \Pr[X \geq a] \leq \frac{\mathbb{E}[X]}{a}$.
In our case $ X$ is counting something (it’s integer valued), so asking whether $ X > 0$ is equivalent to asking whether $ X \geq 1$. The upper bound on the probability of $ X$ being strictly positive is then just $ \mathbb{E}[X]$.
So let’s find out when the expected number of isolated vertices goes to zero. We’ll use the wondrous linearity of expectation to split $ X$ into a sum of counts for each vertex. That is, if $ X_i$ is 1 when vertex $ i$ is isolated and 0 otherwise (this is called an indicator variable), then $ X = \sum_{i=1}^n X_i$ and linearity of expectation gives
$$\displaystyle \mathbb{E}[X] = \mathbb{E}[\sum_{i=1}^n X_i] = \sum_{i=1}^n \mathbb{E}[X_i]$$Now the expectation of an indicator random variable is just the probability that the event occurs (it’s trivial to check). It’s easy to compute the probability that a vertex is isolated: it’s $ (1-p)^n$. So the sum above works out to be $ n(1-p)^n$. It should really be $ n(1-p)^{n-1}$ but the extra factor of $ (1-p)$ doesn’t change anything. The question is what’s the “smallest” way to set $ p$ as a function of $ n$ in order to make the above thing go to zero? Using the fact that $ (1-x) < e^{-x}$ for all $ x > 0$, we get
$$n(1-p)^n < ne^{-pn}$$And setting $ p = (\log n) / n$ simplifies the right hand side to $ ne^{- \log n} = n / n = 1$. This is almost what we want, so let’s set $ p$ to be anything that grows asymptotically faster than $ (\log n) / n$. The notation for this is $ \omega((\log n) / n)$. Then using some slick asymptotic notation we can prove that the RHS of the inequality above goes to zero, and so the LHS must as well. Back to the big picture: we just showed that the expectation of $ X$ (the expected number of isolated vertices) goes to zero, and so by the first moment method the value of $ X$ (the actual number of isolated vertices) has to go to zero with probability tending to 1.
Some quick interpretations: when $ p = (\log n) / n$ each vertex has $ \log n$ neighbors in expectation. Moreover, having no isolated vertices is just a little bit short of the entire graph being connected (our ultimate goal is to figure out exactly when this happens). But already we can see that our conjecture from the beginning is probably false: we aren’t able to use this same method to show that when $ p = c/n$ for some constant $ c$ rules out isolated vertices as $ n \to \infty$. We just got lucky in our data analysis that 5 is about the natural log of 100 (which is 4.6).
The second moment method
Now what about the other side of the coin? If $ p$ is asymptotically less than $ (\log n) / n$ do we necessarily get isolated vertices? That would really put our conjecture to rest. In this case the answer is yes, but it might not be in general. Let’s discuss.
We said that in general if $ \mathbb{E}[X] \to 0$ then the value of $ X$ has to go to zero too (that’s the first moment method). The flip side of this is: if $ \mathbb{E}[X] \to \infty$ does necessarily the value of $ X$ also tend to infinity? The answer is not always yes. Here is a gruesome example I originally heard from a book: say $ X$ is the number of people that will die in the next decade due to an asteroid hitting the earth. The probability that the event happens is quite small, but if it does happen then the number of people that will die is quite large. It is perfectly reasonable for this to drag up the expectation (as the world population grows every decade), but at least we hope a growing population doesn’t by itself increase the value of $ X$.
Mathematics is on our side here. We’re asking under what conditions on $ \mathbb{E}[X]$ does the following implication hold: $ \mathbb{E}[X] \to \infty$ implies $ \Pr[X > 0] \to 1$.
With the first moment method we used Markov’s inequality (a statement about expectation, also called the first moment). With the second moment method we’ll use a statement about the second moment (variances), and the most common is Chebyshev’s inequality. Chebyshev’s inequality states that the probability $ X$ deviates from its expectation by more than $ c$ is bounded by $ \textup{Var}[X] / c^2$. In symbols, for all $ c > 0$ we have
$$\displaystyle \Pr[|X – \mathbb{E}[X]| \geq c] \leq \frac{\textup{Var}[X]}{c^2}$$Now the opposite of $ X > 0$, written in terms of deviation from expectation, is $ |X – \mathbb{E}[X]| \geq \mathbb{E}[X]$. In words, in order for any number $ a$ to be zero, it has to have a distance of at least $ b$ from any number $ b$. It’s such a stupidly simple statement it’s almost confusing. So then we’re saying that
$ \displaystyle \Pr[X = 0] \leq \frac{\textup{Var}[X]}{\mathbb{E}[X]^2}$.
In order to make this probability go to zero, it’s enough to have $ \textup{Var}[X] = o(\mathbb{E}[X]^2)$. Again, the little-o means “grows asymptotically slower than.” So the numerator of the fraction on the RHS will grow asymptotically slower than the denominator, meaning the whole fraction tends to zero. This condition and its implication are together called the “second moment method.”
Great! So we just need to compute $ \textup{Var}[X]$ and check what conditions on $ p$ make it fit the theorem. Recall that $ \textup{Var}[X] = \mathbb{E}[X^2] – \mathbb{E}[X]^2$, and we want to upper bound this in terms of $ \mathbb{E}[X]^2$. Let’s compute $ \mathbb{E}[X]^2$ first.
$$\displaystyle \mathbb{E}[X]^2 = n^2(1-p)^{2n}$$Now the variance.
$$\displaystyle \textup{Var}[X] = \mathbb{E}[X^2] – n^2(1-p)^{2n}$$Expanding $ X$ as a sum of indicator variables $ X_i$ for each vertex, we can split the square into a sum over pairs. Note that $ X_i^2 = X_i$ since they are 0-1 valued indicator variables, and $ X_iX_j$ is the indicator variable for both events happening simultaneously.
$$\displaystyle \begin{aligned} \mathbb{E}[X^2] &= \mathbb{E}[\sum_{i,j} X_{i,j}] \\\ &=\mathbb{E} \left [ \sum_i X_i^2 + \sum_{i \neq j} X_iX_j \right ] \\\ &= \sum_i \mathbb{E}[X_i^2] + \sum_{i \neq j} \mathbb{E}[X_iX_j] \end{aligned}$$By what we said about indicators, the last line is just
$$\displaystyle \sum_i \Pr[i \textup{ is isolated}] + \sum_{i \neq j} \Pr[i,j \textup{ are both isolated}]$$And we can compute each of these pieces quite easily. They are (asymptotically ignoring some constants):
$$\displaystyle n(1-p)^n + n^2(1-p)(1-p)^{2n-4}$$Now combining the two terms together (subtracting off the square of the expectation),
$$\displaystyle \begin{aligned} \textup{Var}[X] &\leq n(1-p)^n + n^2(1-p)^{-3}(1-p)^{2n} – n^2(1-p)^{2n} \\\ &= n(1-p)^n + n^2(1-p)^{2n} \left ( (1-p)^{-3} – 1 \right ) \end{aligned}$$Now we divide by $ \mathbb{E}[X]^2$ to get $ n^{-1}(1-p)^{-n} + (1-p)^{-3} – 1$. Since we’re trying to see if $ p = (\log n) / n$ is a sharp threshold, the natural choice is to let $ p = o((\log n) / n)$. Indeed, using the $ 1-x < e^{-x}$ upper bound and plugging in the little-o bounds the whole quantity by
$$\displaystyle \frac{1}{n}e^{o(\log n)} + o(n^{1/n}) – 1 = o(1)$$i.e., the whole thing tends to zero, as desired.
Other thresholds
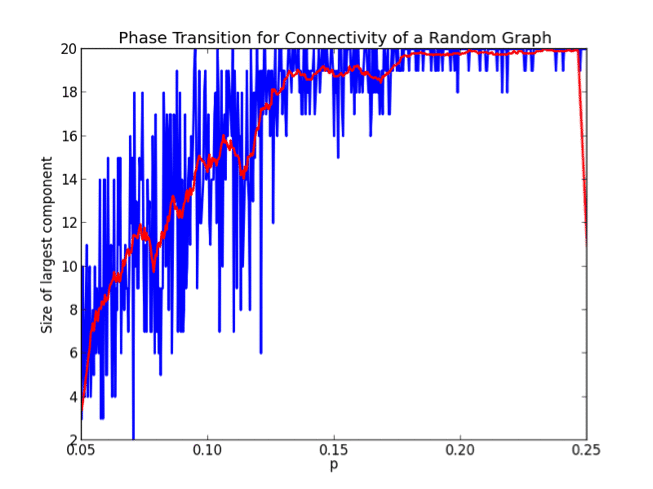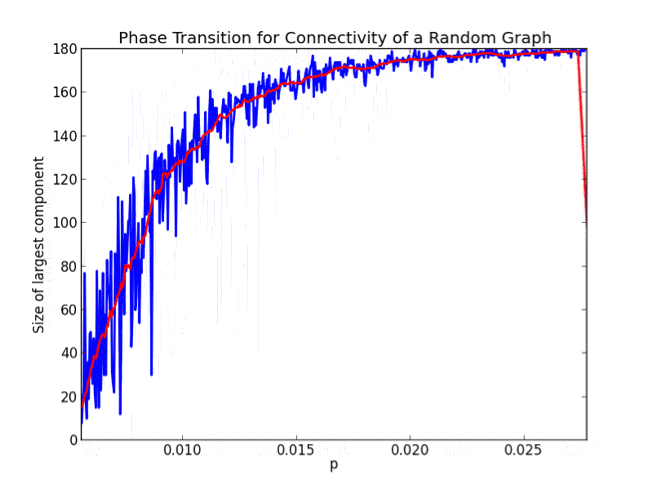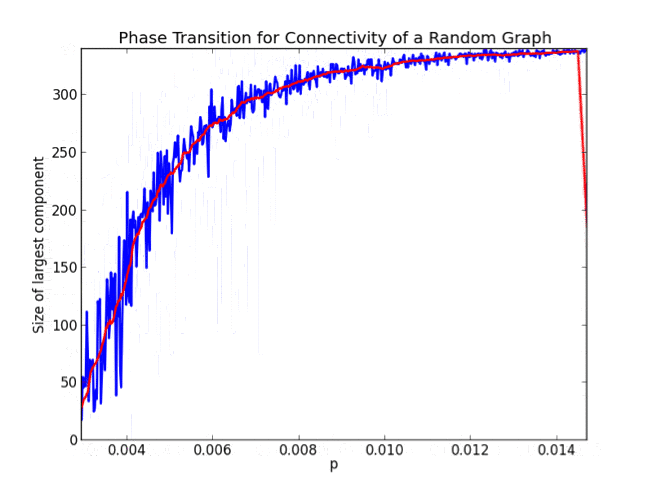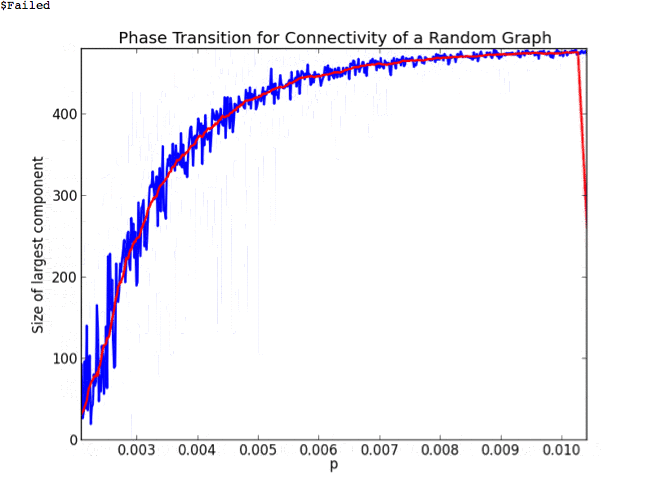
So we just showed that the property of having no isolated vertices in a random graph has a sharp threshold at $ p = (\log n) / n$. Meaning at any larger probability the graph is almost surely devoid of isolated vertices, and at any lower probability the graph almost surely has some isolated vertices.
This might seem like a miracle theorem, but there turns out to be similar theorems for lots of properties. Most of them you can also prove using basically the same method we’ve been using here. I’ll list some below. Also note they are all sharp, two-sided thresholds in the same way that the isolated vertex boundary is.
- The existence of a component of size $ \omega(\log (n))$ has a threshold of $ 1/n$.
- $ p = c/n$ for any $ c > 0$ is a threshold for the existence of a giant component of linear size $ \Theta(n)$. Moreover, above this threshold no other components will have size $ \omega(\log n)$.
- In addition to $ (\log n) / n$ being a threshold for having no isolated vertices, it is also a threshold for connectivity.
- $ p = (\log n + \log \log n + c(n)) / n$ is a sharp threshold for the existence of Hamiltonian cycles in the following sense: if $ c(n) = \omega(1)$ then there will be a Hamilton cycle almost surely, if $ c(n) \to -\infty$ there will be no Hamiltonian cycle almost surely, and if $ c(n) \to c$ the probability of a Hamiltonian cycle is $ e^{-e^{-c}}$. This was proved by Kolmos and Szemeredi in 1983. Moreover, there is an efficient algorithm to find Hamiltonian cycles in these random graphs when they exist with high probability.
Explosive Percolation
So now we know that as the probability of an edge increases, at some point the graph will spontaneously become connected; at some time that is roughly $ \log(n)$ before, the so-called “giant component” will emerge and quickly engulf the entire graph.
Here’s a different perspective on this situation originally set forth by Achlioptas, D’Souza, and Spencer in 2009. It has since become called an “Achlioptas process.”
The idea is that you are watching a random graph grow. Rather than think about random graphs as having a probability above or below some threshold, you can think of it as the number of edges growing (so the thresholds will all be multiplied by $ n$). Then you can imagine that you start with an empty graph, and at every time step someone is adding a new random edge to your graph. Fine, eventually you’ll get so many edges that a giant component emerges and you can measure when that happens.
But now imagine that instead of being given a single random new edge, you are given a choice. Say God presents you with two random edges, and you must pick which to add to your graph. Obviously you will eventually still get a giant component, but the question is how long can you prevent it from occurring? That is, how far back can we push the threshold for connectedness by cleverly selecting the new edge?
What Achlioptas and company conjectured was that you can push it back (some), but that when you push it back as far as it can go, the threshold becomes discontinuous. That is, they believed there was a constant $ \delta \geq 1/2$ such that the size of the largest component jumps from $ o(n)$ to $ \delta n$ in $ o(n)$ steps.
This turned out to be false, and Riordan and Warnke proved it. Nevertheless, the idea has been interpreted in an interesting light. People have claimed it is a useful model of disaster in the following sense. If you imagine that an edge between two vertices is a “crisis” relating two entities. Then in every step God presents you with two crises and you only have the resources to fix one. The idea is that when the entire graph is connected, you have this one big disaster where all the problems are interacting with each other. The percolation process describes how long you can “survive” while avoiding the big disaster.
There are critiques of this interpretation, though, mainly about how simplistic it is. In particular, an Achlioptas process models a crisis as an exogenous force when in reality problems are usually endogenous. You don’t expect a meteor to hit the Earth, but you do expect humans to have an impact on the environment. Also, not everybody in the network is trying to avoid errors. Some companies thrive in economic downturns by managing your toxic assets, for example. So one could reasonably argue that Achlioptas processes aren’t complex enough to model the realistic types of disasters we face.
Either way, I find it fantastic that something like a random graph (which for decades was securely in pure combinatorics away from applications) is spurring such discussion.
Next time, we’ll take one more dive into the theory of Erdős-Rényi random graphs to prove a very “meta” theorem about sharp thresholds. Then we’ll turn our attention to other models of random graphs, hopefully more realistic ones 🙂
Until then!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.