So here we are. We’ve studied the general properties of elliptic curves, written a program for elliptic curve arithmetic over the rational numbers, and taken a long detour to get some familiarity with finite fields (the mathematical background and a program that implements arbitrary finite field arithmetic).
And now we want to get back on track and hook our elliptic curve program up with our finite field program to make everything work. And indeed, for most cases it’s just that simple! For example, take the point $ P = (2,1)$ on the elliptic curve $ y = x^3 + x + 1$ with coefficients in $ \mathbb{Z}/5$. Using purely code produced in previous posts, we can do arithmetic:
>>> F5 = FiniteField(5, 1)
>>> C = EllipticCurve(a=F5(1), b=F5(1))
>>> P = Point(C, F5(2), F5(1))
>>> P
(2 (mod 5), 1 (mod 5))
>>> 2*P
(2 (mod 5), 4 (mod 5))
>>> 3*P
Ideal
Here’s an example of the same curve $ y^2 = x^3 + x + 1$ with coefficients over the finite field of order 25 $ \mathbb{F}_{5^2}$.
>>> F25 = FiniteField(5,2)
>>> F25.idealGenerator
3 + 0 t^1 + 1 t^2
>>> curve = EllipticCurve(a=F25([1]), b=F25([1]))
>>> x = F25([2,1])
>>> y = F25([0,2])
>>> y*y - x*x*x - x - 1
0 ∈ F_{5^2}
>>> curve.testPoint(x,y)
True
>>> P = Point(curve, x, y)
>>> -P
(2 + 1 t^1, 0 + 3 t^1)
>>> P+P
(3 + 1 t^1, 2)
>>> 4*P
(3 + 2 t^1, 4 + 4 t^1)
>>> 9*P
Ideal
There are some subtle issues, though, in that we shouldn’t use the code we have to work over any finite field. But we’ve come very far and covered a lot of technical details, so let’s briefly remember how we got here.
Taking a Step Back
At the beginning there was only $ \mathbb{Q}$, the field of rational numbers. We had a really nice geometric picture of elliptic curves over this field, and using that picture we developed an algorithm for (geometrically) adding points.
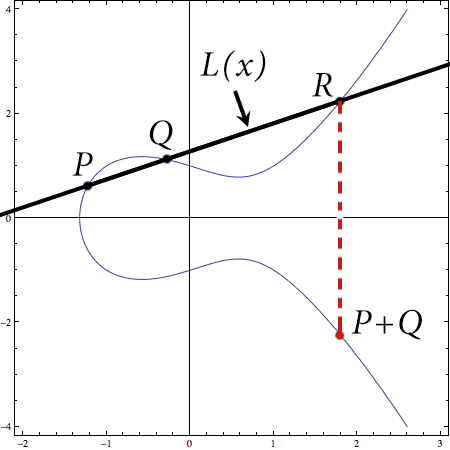
add-points-example
If we assume the equation of the elliptic curve had this nice form (the so-called Weierstrass normal form, $ y^2 = x^3 + ax + b$), then we were able to translate the geometric algorithm into an algebraic one. This made it possible to write a program to perform the additions, and this was our first programmatic milestone. Along the way, we learned about groups and projective geometry, which I explained was the proper mathematical setting for elliptic curves. In that setting, we saw that for most fields, every elliptic curve could be modified into one in Weierstrass normal form without changing the algebraic structure of the set of solutions. Moreover, we saw that you can replace the field $ \mathbb{Q}$ with the field of your choice. The set of solutions to an elliptic curve still forms a group and the same algebraic point-adding algorithm works. It’s just an interesting quirk of mathematics that one way to represent elements of finite fields are as polynomial remainders when dividing by a “prime” polynomial (analogous to modular arithmetic with integers). So we spent a while actually implementing finite fields in terms of this representation.
The reader has probably heard of this, but in practice one uses a (very large) finite field for the coefficients of their elliptic curve. Often this is $ \mathbb{Z}/p$ for some really large prime $ p$, or the field of $ 2^m$ elements for some large integer $ m$. But one would naturally complain: there are so many (infinitely many!) finite fields to choose from! Which one should we use, and how did they choose these?
As with most engineering problems the answer is a trade-off, in this case between efficiency and security. Arithmetic is faster in fields of characteristic 2 (and easy to implement at the hardware level!) but a lot is known about the finite field of $ 2^m$ elements. In fact, if you are sloppy in picking $ m$ you’ll get no security at all! One prominent example is the so-called Weil descent attack, which breaks security assumptions for elliptic curve cryptography when $ m$ is not prime. These attacks use some sophisticated machinery, but this is how it goes. An abstract mathematical breakthrough can immediately invalidate cryptography based on certain elliptic curves.
But before we get neck-deep in cryptography we have an even bigger problem: for some finite fields, not every elliptic curve has a Weierstrass normal form! So our program isn’t expressive enough to represent all elliptic curves we might want to. We could avoid these curves in our applications, but that would be unnecessarily limiting. With a bit more careful work, we can devise a more general algorithm (and a different normal form) that works for all fields. But let’s understand the problem first.
In general, you can have an elliptic curve of the form $ \sum_{i+j=3} a_{i,j}x^iy^j = 0$. That is, it’s just a really general degree 3 polynomial in two variables. If we assume the discriminant of this polynomial is nonzero, we’ll get a smooth curve. And then to get to the Weierstrass normal form involves a bunch of changes of variables. The problem is that the algebraic manipulations you do require you to multiply and divide by 2 and 3. In a field of either characteristic, these operations are either destructive (multiplying by zero) or totally illegal (dividing by zero), and they ruin Weierstrass’s day.
So what can we do?
Well it turns out that there is a more general Weierstrass normal form, unsurprisingly called the generalized Weierstrass normal form. It looks like this
$$\displaystyle y^2 + a_1 xy + a_3y = x^3 + a_2x^2 + a_4x + a_6$$The same geometric idea of drawing lines works for this curve as well. It’s just that now the formula is way more complicated. It involves computing a bunch of helper constants and computing far more arithmetic. My colleague Daniel Ngheim was kind enough to code up the algorithm, and here it is
def __add__(self, Q):
if isinstance(Q, Ideal):
return Point(self.curve, self.x, self.y)
a1,a2,a3,a4,a6 = (self.curve.a1, self.curve.a2, self.curve.a3, self.curve.a4, self.curve.a6)
if self.x == Q.x:
x = self.x
if self.y + Q.y + a1*x + a3 == 0:
return Ideal(self.curve)
else:
c = ((3*x*x + 2*a2*x + a4 - a1*self.y) / (2*self.y + a1*x + a3))
d = (-(x*x*x) + a4*x + 2*a6 - a3*self.y) / (2*self.y + a1*x + a3)
Sum_x = c*c + a1*c - a2 - 2*self.x
Sum_y = -(c + a1) * Sum_x - d - a3
return Point(self.curve, Sum_x, Sum_y)
else:
c = (Q.y - self.y) / (Q.x - self.x)
d = (self.y*Q.x - Q.y*self.x) / (Q.x - self.x)
Sum_x = c*c + a1*c - a2 - self.x - Q.x
Sum_y = -(c + a1)*Sum_x - d - a3
return Point(self.curve, Sum_x, Sum_y)
def __neg__(self):
return Point(self.curve, self.x, -self.y - self.curve.a1*self.x - self.curve.a3)
I trust that the devoted reader could derive this algorithm by hand, but for a more detailed derivation see the book of Silverman (it’s a graduate level text, but the point is that if you’re not really serious about implementing elliptic curve cryptography then you shouldn’t worry about this more general algorithm).
One might start to wonder: are there still other forms of elliptic curves that we could use to get around some of the difficulties of the Weierstrass normal form? The answer is yes, but we’ll defer their discussion to a future post. The brief explanation is that through a different choice of variable changes you can get to a different form of curve, and the algorithms you get from writing out the algebraic equations for adding points are slightly more efficient.
For the remainder of this series we’ll just work with one family of finite fields, those fields of the form $ \mathbb{Z}/p$ for some large $ p$. There is one particularly famous elliptic curve over this field that is used in some of the most secure applications in existence, and this will roughly be our target. In either case, we have provided the combined elliptic curve and finite field code (and the generalized elliptic curve class) on this blog’s Github page.
So in the next post we’ll actually start talking about cryptography and how to use elliptic curves to do things like generate a shared secret key.
Until then!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.