In the last twenty years there has been a lot of research in a subfield of machine learning called Bandit Learning. The name comes from the problem of being faced with a large sequence of slot machines (once called one-armed bandits) each with a potentially different payout scheme. The problems in this field all focus on one central question:
If I have many available actions with uncertain outcomes, how should I act to maximize the quality of my results over many trials?
The deep question here is how to balance exploitation, the desire to choose an action which has payed off well in the past, with exploration, the desire to try options which may produce even better results. The ideas are general enough that it’s hard not to find applications: choosing which drug to test in a clinical study, choosing which companies to invest in, choosing which ads or news stories to display to users, and even (as Richard Feynman once wondered) how to maximize your dining enjoyment.
Herbet Robbins, one of the first to study bandit learning algorithms.
In less recent times (circa 1960’s), this problem was posed and considered in the case where the payoff mechanisms had a very simple structure: each slot machine is a coin flip with a different probability $ p$ of winning, and the player’s goal is to find the best machine as quickly as possible. We called this the “stochastic” setting, and last time we saw a modern strategy called UCB1 which maintained statistical estimates on the payoffs of the actions and chose the action with the highest estimate. The underlying philosophy was “optimism in the face of uncertainty,” and it gave us something provably close to optimal.
Unfortunately payoff structures are more complex than coin flips in the real world. Having “optimism” is arguably naive, especially when it comes to competitive scenarios like stock trading. Indeed the algorithm we’ll analyze in this post will take the polar opposite stance, that payoffs could conceivably operate in any manner. This is called the adversarial model, because even though the payoffs are fixed in advance of the game beginning, it can always be the case that the next choice you make results in the worst possible payoff.
One might wonder how we can hope to do anything in such a pessimistic model. As we’ll see, our notion of performing well is relative to the best single slot machine, and we will argue that this is the only reasonable notion of success. On the other hand, one might argue that real world payoffs are almost never entirely adversarial, and so we would hope that algorithms which do well theoretically in the adversarial model excel beyond their minimal guarantees in practice.
In this post we’ll explore and implement one algorithm for adversarial bandit learning, called Exp3, and in the next post we’ll see how it fares against UCB1 in some applications. Some prerequisites: since the main algorithm presented in this post is randomized, its analysis requires some familiarity with techniques and notation from probability theory. Specifically, we will assume that the reader is familiar with the content of this blog’s basic probability theory primers (1, 2), though the real difficulty in the analysis will be keeping up with all of the notation.
In case the reader is curious, Exp3 was invented in 2001 by Auer, Cesa-Bianchi, Freund, and Schapire. Here is their original paper, which contains lots of other mathematical goodies.
As usual, all of the code and data produced in the making of this blog post is available for download on this blog’s Github page.
Model Formalization and Notions of Regret
Before we describe the algorithm and analyze its we have to set up the problem formally. The first few paragraphs of our last post give a high-level picture of general bandit learning, so we won’t repeat that here. Recall, however, that we have to describe both the structure of the payoffs and how success is measured. So let’s describe the former first.
Definition: An adversarial bandit problem is a pair $ (K, \mathbf{x})$, where $ K$ represents the number of actions (henceforth indexed by $ i$), and $ \mathbf{x}$ is an infinite sequence of payoff vectors $ \mathbf{x} = \mathbf{x}(1), \mathbf{x}(2), \dots$, where $ \mathbf{x}(t) = (x_1(t), \dots, x_K(t))$ is a vector of length $ K$ and $ x_i(t) \in [0,1]$ is the reward of action $ i$ on step $ t$.
In English, the game is played in rounds (or “time steps”) indexed by $ t = 1, 2, \dots$, and the payoffs are fixed for each action and time before the game even starts. Note that we assume the reward of an action is a number in the interval $ [0,1]$, but all of our arguments in this post can be extended to payoffs in some range $ [a,b]$ by shifting by $ a$ and dividing by $ b-a$.
Let’s specify what the player (algorithm designer) knows during the course of the game. First, the value of $ K$ is given, and total number of rounds is kept secret. In each round, the player has access to the history of rewards for the actions that were chosen by the algorithm in previous rounds, but not the rewards of unchosen actions. In other words, it will only ever know one $ x_i(t)$ for each $ t$. To set up some notation, if we call $ i_1, \dots, i_t$ the list of chosen actions over $ t$ rounds, then at step $ t+1$ the player has access to the values of $ x_{i_1}(1), \dots, x_{i_t}(t)$ and must pick $ i_{t+1}$ to continue.
So to be completely clear, the game progresses as follows:
The player is given access to $ K$. For each time step $ t$:
The player must pick an action $ i_t$. The player observes the reward $ x_i(t) \in [0,1]$, which he may save for future use.
The problem gives no explicit limit on the amount of computation performed during each step, but in general we want it to run in polynomial time and not depend on the round number $ t$. If runtime even logarithmically depended on $ t$, then we’d have a big problem using it for high-frequency applications. For example in ad serving, Google processes on the order of $ 10^9$ ads per day; so a logarithmic dependence wouldn’t be that bad, but at some point in the distance future Google wouldn’t be able to keep up (and we all want long-term solutions to our problems).
Note that the reward vectors $ \mathbf{x}_t$ must be fixed in advance of the algorithm running, but this still allows a lot of counterintuitive things. For example, the payoffs can depend adversarially on the algorithm the player decides to use. For example, if the player chooses the stupid strategy of always picking the first action, then the adversary can just make that the worst possible action to choose. However, the rewards cannot depend on the random choices made by the player during the game.
So now let’s talk about measuring success. For an algorithm $ A$ which chooses the sequence $ i_1, \dots, i_t$ of actions, define $ G_A(t)$ to be the sum of the observed rewards
$ \displaystyle G_A(t) = \sum_{s=1}^t x_{i_s}(s)$.
And because $ A$ will often be randomized, this value is a random variable depending on the decisions made by $ A$. As such, we will often only consider the payoff up to expectation. That is, we’ll be interested in how $ \textup{E}(G_A(t))$ relates to other possible courses of action. To be completely rigorous, the randomization is not over “choices made by an algorithm,” but rather the probability distribution over sequences of actions that the algorithm induces. It’s a fine distinction but a necessary one. In other words, we could define any sequence of actions $ \mathbf{j} = (j_1, \dots, j_t)$ and define $ G_{\mathbf{j}}(t)$ analogously as above:
$ \displaystyle G_{\mathbf{j}}(t) = \sum_{s=1}^t x_{j_s}(s)$.
Any algorithm and choice of reward vectors induces a probability distribution over sequences of actions in a natural way (if you want to draw from the distribution, just run the algorithm). So instead of conditioning our probabilities and expectations on previous choices made by the algorithm, we do it over histories of actions $ i_1, \dots, i_t$.
An obvious question we might ask is: why can’t the adversary just make all the payoffs zero? (or negative!) In this event the player won’t get any reward, but he can emotionally and psychologically accept this fate. If he never stood a chance to get any reward in the first place, why should he feel bad about the inevitable result? What a truly cruel adversary wants is, at the end of the game, to show the player what he could have won, and have it far exceed what he actually won. In this way the player feels regret for not using a more sensible strategy, and likely turns to binge eating cookie dough ice cream. Or more likely he returns to the casino to lose more money. The trick that the player has up his sleeve is precisely the randomness in his choice of actions, and he can use its objectivity to partially overcome even the nastiest of adversaries.

The adversary would love to show you this bluff after you choose to fold your hand. What a jerk.
Sadism aside, this thought brings us to a few mathematical notions of regret that the player algorithm may seek to minimize. The first, most obvious, and least reasonable is the worst-case regret. Given a stopping time $ T$ and a sequence of actions $ \mathbf{j} = (j_1, \dots, j_T)$, the expected regret of algorithm $ A$ with respect to $ \mathbf{j}$ is the difference $ G_{\mathbf{j}}(T) – \mathbb{E}(G_A(T))$. This notion of regret measures the regret of a player if he knew what would have happened had he played $ \mathbf{j}$. The expected worst-case regret of $ A$ is then the maximum over all sequences $ \mathbf{j}$ of the regret of $ A$ with respect to $ \mathbf{j}$. This notion of regret seems particularly unruly, especially considering that the payoffs are adversarial, but there are techniques to reason about it.
However, the focus of this post is on a slightly easier notion of regret, called weak regret, which instead compares the results of $ A$ to the best single action over all rounds. That is, this quantity is just
$$\displaystyle \left ( \max_{j} \sum_{t=1}^T x_j(t) \right ) – \mathbb{E}(G_A(T))$$We call the parenthetical term $ G_{\textup{max}}(T)$. This kind of regret is a bit easier to analyze, and the main theorem of this post will given an upper bound on it for Exp3. The reader who read our last post on UCB1 will wonder why we make a big distinction here just to arrive at the same definition of regret that we had in the stochastic setting. But with UCB1 the best sequence of actions to take just happened to be to play the best action over and over again. Here, the payoff difference between the best sequence of actions and the best single action can be arbitrarily large.
Exp3 and an Upper Bound on Weak Regret
We now describe at the Exp3 algorithm.
Exp3 stands for Exponential-weight algorithm for Exploration and Exploitation. It works by maintaining a list of weights for each of the actions, using these weights to decide randomly which action to take next, and increasing (decreasing) the relevant weights when a payoff is good (bad). We further introduce an egalitarianism factor $ \gamma \in [0,1]$ which tunes the desire to pick an action uniformly at random. That is, if $ \gamma = 1$, the weights have no effect on the choices at any step.
The algorithm is readily described in Python code, but we need to set up some notation used in the proof of the theorem. The pseudocode for the algorithm is as follows.
Exp3
- Given $ \gamma \in [0,1]$, initialize the weights $ w_i(1) = 1$ for $ i = 1, \dots, K$.
- In each round $ t$:
- Set $ \displaystyle p_i(t) = (1-\gamma)\frac{w_i(t)}{\sum_{j=1}^K w_j(t)} + \frac{\gamma}{K}$ for each $ i$.
- Draw the next action $ i_t$ randomly according to the distribution of $ p_i(t)$.
- Observe reward $ x_{i_t}(t)$.
- Define the estimated reward $ \hat{x}_{i_t}(t)$ to be $ x_{i_t}(t) / p_{i_t}(t)$.
- Set $ \displaystyle w_{i_t}(t+1) = w_{i_t}(t) e^{\gamma \hat{x}_{i_t}(t) / K}$
- Set all other $ w_j(t+1) = w_j(t)$.
The choices of these particular mathematical quantities (in steps 1, 4, and 5) are a priori mysterious, but we will explain them momentarily. In the proof that follows, we will extend $ \hat{x}_{i_t}(t)$ to indices other than $ i_t$ and define those values to be zero.
The Python implementation is perhaps more legible, and implements the possibly infinite loop as a generator:
def exp3(numActions, reward, gamma):
weights = [1.0] * numActions
t = 0
while True:
probabilityDistribution = distr(weights, gamma)
choice = draw(probabilityDistribution)
theReward = reward(choice, t)
estimatedReward = 1.0 * theReward / probabilityDistribution[choice]
weights[choice] *= math.exp(estimatedReward * gamma / numActions) # important that we use estimated reward here!
yield choice, theReward, estimatedReward, weights
t = t + 1
Here the “rewards” variable refers to a callable which accepts as input the action chosen in round $ t$ (keeps track of $ t$, assuming we’ll play nice), and returns as output the reward for that choice. The distr and draw functions are also easily defined, with the former depending on the gamma parameter as follows:
def distr(weights, gamma=0.0):
theSum = float(sum(weights))
return tuple((1.0 - gamma) * (w / theSum) + (gamma / len(weights)) for w in weights)
There is one odd part of the algorithm above, and that’s the “estimated reward” $ \hat{x}_{i_t}(t) = x_{i_t}(t) / p_{i_t}(t)$. The intuitive reason to do this is to compensate for a potentially small probability of getting the observed reward. More formally, it ensures that the conditional expectation of the “estimated reward” is the actual reward. We will explore this formally during the proof of the main theorem.
As usual, the programs we write in this post are available on this blog’s Github page.
We can now state and prove the upper bound on the weak regret of Exp3. Note all logarithms are base $ e$.
Theorem: For any $ K > 0, \gamma \in (0, 1]$, and any stopping time $ T \in \mathbb{N}$
$ \displaystyle G_{\textup{max}}(T) – \mathbb{E}(G_{\textup{Exp3}}(T)) \leq (e-1)\gamma G_{\textup{max}}(T) + \frac{K \log K}{\gamma}$.
This is a purely analytical result because we don’t actually know what $ G_{\textup{max}}(T)$ is ahead of time. Also note how the factor of $ \gamma$ occurs: in the first term, having a large $ \gamma$ will result in a poor upper bound because it occurs in the numerator of that term: too much exploration means not enough exploitation. But it occurs in the denominator of the second term, meaning that not enough exploration can also produce an undesirably large regret. This theorem then provides a quantification of the tradeoff being made, although it is just an upper bound.
Proof.
We present the proof in two parts. Part 1:
We made a notable mistake in part 1, claiming that $ e^x \leq 1 + x + (e-2)x^2$ when $ x \leq 1$. In fact, this does follow from the Taylor series expansion of $ e$, but it’s not as straightforward as I made it sound. In particular, note that $ e^x = 1 + x + \frac{x^2}{2!} + \dots$, and so $ e^1 = 2 + \sum_{k=2}^\infty \frac{1}{k!}$. Using $ (e-2)$ in place of $ \frac{1}{2}$ gives
$$\displaystyle 1 + x + \left ( \sum_{k=2}^{\infty} \frac{x^2}{k!} \right )$$And since $ 0 < x \leq 1$, each term in the sum will decrease when replaced by $ \frac{x^k}{k!}$, and we’ll be left with exactly $ e^x$. In other words, this is the tightest possible quadratic upper bound on $ e^x$. Pretty neat! On to part 2:
As usual, here is the entire canvas made over the course of both videos.
$$\square$$We can get a version of this theorem that is easier to analyze by picking a suitable choice of $ \gamma$.
Corollary: Assume that $ G_{\textup{max}}(T)$ is bounded by $ g$, and that Exp3 is run with
$$\displaystyle \gamma = \min \left ( 1, \sqrt{\frac{K \log K}{(e-1)g}} \right )$$Then the weak regret of Exp3 is bounded by $ 2.63 \sqrt{g K \log K}$ for any reward vector $ \mathbf{x}$.
Proof. Simply plug $ \gamma$ in the bound in the theorem above, and note that $ 2 \sqrt{e-1} < 2.63$.
A Simple Test Against Coin Flips
Now that we’ve analyzed the theoretical guarantees of the Exp3 algorithm, let’s use our implementation above and see how it fares in practice. Our first test will use 10 coin flips (Bernoulli trials) for our actions, with the probabilities of winning (and the actual payoff vectors) defined as follows:
biases = [1.0 / k for k in range(2,12)]
rewardVector = [[1 if random.random() < bias else 0 for bias in biases] for _ in range(numRounds)]
rewards = lambda choice, t: rewardVector[t][choice]
If we are to analyze the regret of Exp3 against the best action, we must compute the payoffs for all actions ahead of time, and compute which is the best. Obviously it will be the one with the largest probability of winning (the first in the list generated above), but it might not be, so we have to compute it. Specifically, it’s the following argmax:
bestAction = max(range(numActions), key=lambda action: sum([rewardVector[t][action] for t in range(numRounds)]))
Where the max function is used as “argmax” would be in mathematics.
We also have to pick a good choice of $ \gamma$, and the corollary from the previous section gives us a good guide to the optimal $ \gamma$: simply find a good upper bound on the reward of the best action, and use that. We can cheat a little here: we know the best action has a probability of 1/2 of paying out, and so the expected reward if we always did the best action is half the number of rounds. If we use, say, $ g = 2T / 3$ and compute $ \gamma$ using the formula from the corollary, this will give us a reasonable (but perhaps not perfectly correct) upper bound.
Then we just run the exp3 generator for $ T = \textup{10,000}$ rounds, and compute some statistics as we go:
bestUpperBoundEstimate = 2 * numRounds / 3
gamma = math.sqrt(numActions * math.log(numActions) / ((math.e - 1) * bestUpperBoundEstimate))
gamma = 0.07
cumulativeReward = 0
bestActionCumulativeReward = 0
weakRegret = 0
t = 0
for (choice, reward, est, weights) in exp3(numActions, rewards, gamma):
cumulativeReward += reward
bestActionCumulativeReward += rewardVector[t][bestAction]
weakRegret = (bestActionCumulativeReward - cumulativeReward)
regretBound = (math.e - 1) * gamma * bestActionCumulativeReward + (numActions * math.log(numActions)) / gamma
t += 1
if t >= numRounds:
break
At the end of one run of ten thousand rounds, the weights are overwhelmingly in favor of the best arm. The cumulative regret is 723, compared to the theoretical upper bound of 897. It’s not too shabby, but by tinkering with the value of $ \gamma$ we see that we can get regrets lower than 500 (when $ \gamma$ is around 0.7). Considering that the cumulative reward for the player is around 4,500 in this experiment, that means we spent only about 500 rounds out of ten thousand exploring non-optimal options (and also getting unlucky during said exploration). Not too shabby at all.
Here is a graph of a run of this experiment.
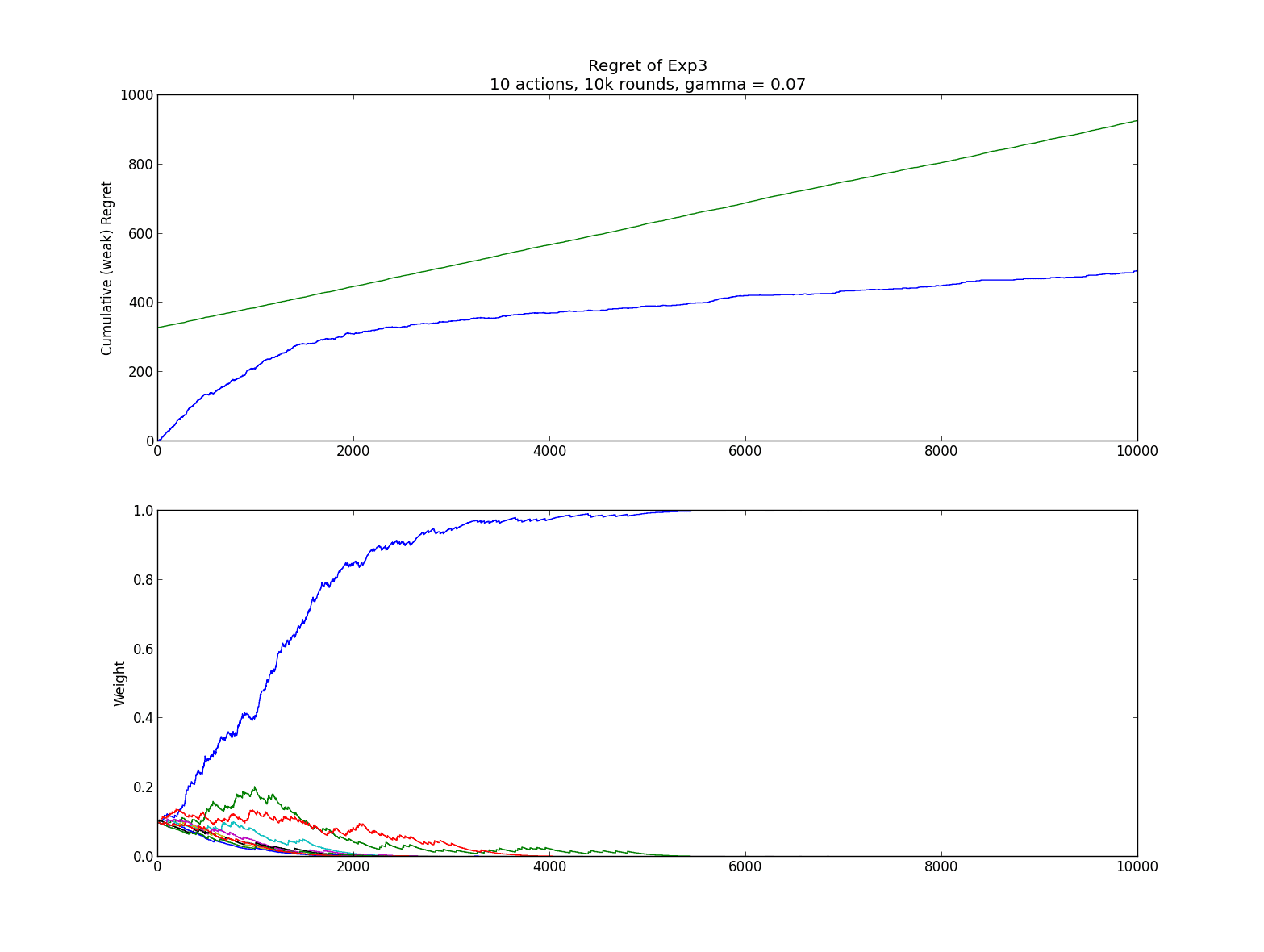
exp3-regret-graph
Note how the Exp3 algorithm never stops increasing its regret. This is in part because of the adversarial model; even if Exp3 finds the absolutely perfect action to take, it just can’t get over the fact that the world might try to screw it over. As long as the $ \gamma$ parameter is greater than zero, Exp3 will explore bad options just in case they turn out to be good. The benefits of this is that if the model changes over time Exp3 will adapt, but the downside is that the pessimism inherent in this worldview generally results in lower payoffs than other algorithms.
More Variations, and Future Plans
Right now we have two contesting models of how the world works: is it stochastic and independent, like the UCB1 algorithm would optimize for? Or does it follow Exp3’s world view that the payoffs are adversarial? Next time we’ll run some real-world tests to see how each fares.
But before that, we should note that there are still more models we haven’t discussed. One extremely significant model is that of contextual bandits. That is, the real world settings we care about often come with some “context” associated with each trial. Ads being displayed to users have probabilities that should take into account the information known about the user, and medical treatments should take into account past medical history. While we will not likely investigate any contextual bandit algorithms on this blog in the near future, the reader who hopes to apply this work to his or her own exploits (no pun intended) should be aware of the additional reading.
Until next time!
Postscript: years later, a cool post by Tim Vieira shows a neat data structure that asymptotically speeds up the update/sample step of the EXP3 algorithm from linear to logarithmic (among others). The weights are stored in a heap of partial sums (the leaves are the individual weights), and sampling is a binary search. See the original post and the accompanying gist for an implementation. Exercise: implement the data structure for use with our EXP3 implementation.
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.