A lot of people who like functional programming often give the reason that the functional style is simply more elegant than the imperative style. When compelled or inspired to explain (as I did in my old post, How I Learned to Love Functional Programming), they often point to the three “higher-order” functions map, fold, and filter, as providing a unifying framework for writing and reasoning about programs. But how unifying are they, really? In this post we’ll give characterizations of these functions in terms of universal properties, and we’ll see that in fact fold is the “most” universal of the three, and its natural generalization gives a characterization of transformations of standard compound data types.
By being universal or having a universal property, we don’t mean that map, fold, and filter are somehow mystically connected to all programming paradigms. That might be true, but it’s not the point of this article. Rather, by saying something has a universal property we are making a precise mathematical statement that it is either an initial or final object (or the unique morphism determined by such) in some category.
That means that, as a fair warning to the reader, this post assumes some basic knowledge of category theory, but no more than what we’ve covered on this blog in the past. Of particular importance for the first half of this post is the concept of a universal property, and in the followup post we’ll need some basic knowledge of functors.
Map, Filter, and Fold
Recalling their basic definitions, map is a function which accepts as input a list $ L$ whose elements all have the same type (call it $ A$), and a function $ f$ which maps $ A$ to another type $ B$. Map then applies $ f$ to every entry of $ L$ to produce a new list whose entries all have type $ B$.
In most languages, implementing the map function is an elementary exercise. Here is one possible definition in ML.
fun map(_, nil) = nil
| map(f, (head::tail)) = f(head) :: map(f, tail)
Next, filter takes as input a boolean-valued predicate $ p : A \to \textup{bool}$ on types $ A$ and a list $ L$ whose entries have type $ A$, and produces a list of those entries of $ L$ which satisfy the predicate. Again, it’s implementation in ML might be:
fun filter(_, nil) = nil
| filter(p, (head::tail)) = if p(head)
then (head :: filter(p, tail))
else filter(p, tail)
Finally, fold is a function which “reduces” a list $ L$ of entries with type $ A$ down to a single value of type $ B$. It accepts as input a function $ f : A \times B \to B$, and an initial value $ v \in B$, and produces a value of type $ B$ by recursively applying $ f$ as follows:
fun fold(_, v, nil) = v
| fold(f, v, (head::tail)) = f(head, fold(f, v, tail))
(If this definition is mysterious, you’re probably not ready for the rest of this post.)
One thing that’s nice about fold is that we can define map and filter in terms of it:
fun map(f, L) = fold((fn x, xs => (f(x):xs)), [], L)
fun filter(p, L) = fold((fn x, xs => if p(x) then x:xs else xs end), [], L)
We’ll see that this is no accident: fold happens to have the “most general” universality of the three functions, but as a warm-up and a reminder we first investigate the universality of map and filter.
Free Monoids and Map
Map is the easiest function of the three to analyze, but to understand it we need to understand something about monoids. A monoid is simple to describe, it’s just a set $ M$ with an associative binary operation denoted by multiplication and an identity element for that operation.
A monoid homomoprhism between two monoids $ M, N$ is a function $ f: M \to N$ such that $ f(xy) = f(x)f(y)$. Here the multiplication on the left hand side of the equality is the operation from $ M$ and on the right it’s the one from $ N$ (this is the same definition as a group homomorphism). As is to be expected, monoids with monoid homomorphisms form a category.
We encounter simple monoids every day in programming which elucidate this definition. Strings with the operation of string concatenation form a monoid, and the empty string acts as an identity because concatenating a string to the empty string has no effect. Similarly, lists with list concatenation form a monoid, where the identity is the empty list. A nice example of a monoid homomorphism is the length function. We know it’s a homomorphism because the length of a concatenation of two lists is just the sum of the lengths of the two lists.
Integers also form a monoid, with addition as the operation and zero as the identity element. However, the list and string monoids have an extra special property that integers do not. For a number $ n$ you can always find $ -n$ so that $ n + (-n) = 0$ is the identity element. But for lists, the only way to concatenate two lists and get the empty list is if both of the lists were empty to begin with. A monoid with this property is called free, and to fully understand it we should make a definition which won’t seem to mean anything at first.
Definition: Let $ \mathbf{C}$ be a category. Given a set $ A$, the free object over $ A$, denoted $ F(A)$, is an object of $ \mathbf{C}$ which is universal with respect to set-maps $ A \to B$ for any object $ B$ in $ \mathbf{C}$.
As usual with a definition by universal property, we should elaborate as to exactly what’s going on. Let $ \mathbf{C}$ be a category whose objects are sets and let $ A$ a set, possibly not in this category. We can construct a new category, $ \mathbf{C}_{A \to X}$ whose objects are set-maps
$$\displaystyle f: A \to X$$and whose morphisms are commutative diagrams of the form
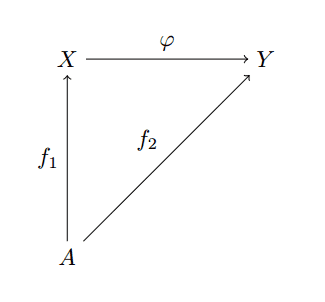
free-object-cat-morphism
where $ \varphi$ is a morphism in $ \mathbf{C}$. In other words, we simply require that $ \varphi(f_1(a)) = f_2(a)$ for every $ a \in A$.
By saying that the free monoid on $ A$ satisfies this universal property for the category of monoids, we really mean that it is initial in this category of set-maps and commutative diagrams. That is, there is a monoid $ F(A)$ and a set-map $ i_A: A \to F(A)$ so that for every monoid $ Y$ and set-map $ f: A \to Y$ there is a unique monoid homomorphism from $ i_A$ to $ f$. In other words, there is a unique monoid homomorphism $ \varphi$ making the following diagram commute:
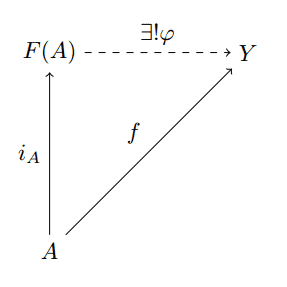
free-object-univ-prop
For example, if $ A$ is the set of all unicode characters, then $ F(A)$ is precisely the monoid of all strings on those characters. The map $ i_A$ is then the map taking a character $ a$ to the single-character string “$ a$”. More generally, if $ T$ is any type in the category of types and computable functions, then $ F(T)$ is the type of homogeneous lists whose elements have type $ T$.
We will now restrict our attention to lists and types, and we will denote the free (list) monoid on a type $ A$ as $ [A]$. The universal property of map is then easy to describe, it’s just a specific instance of this more general universal property for the free monoids. Specifically, we work in the sub-category of homogeneous list monoids (we only allow objects which are $ [T]$ for some type $ T$). The morphism $ i_A: A \to [A]$ just takes a value $ a$ of type $ A$ and spits out a single-item list $ [a]$. We might hope that for any mapping $ A \to [B]$, there is a unique monoid homomorphism $ [A] \to [B]$ making the following diagram commute.
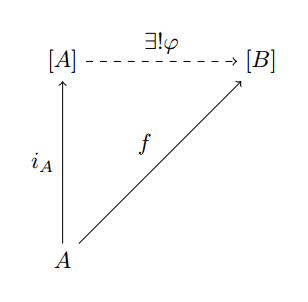
bad-map
And while this is true, the diagram lies because “map” does not achieve what $ \varphi$ does. The map $ f$ might send all of $ A$ to the empty list, and this would cause $ \varphi$ to be the trivial map. But if we decomposed $ f$ further to require it to send $ a$ to a single $ b$, such as
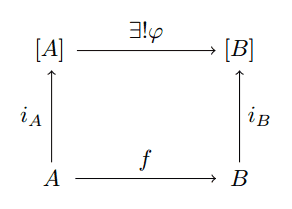
still-bad-map
then things work out nicely. In particular, specifying a function $ f: A \to B$ uniquely defines how a list homomorphism operates on lists. In particular, the diagram forces the behavior for single-element lists: $ [a] \mapsto [f(a)]$. And the property of $ \varphi$ being a monoid homomorphism forces $ \varphi$ to preserve order.
Indeed, we’ve learned from this analysis that the structure of the list involved is crucial in forming the universal property. Map is far from the only computable function making the diagram commute, but it is clearly the only monoid homomorphism. As we’ll see, specifying the order of operations is more generally described by fold, and we’ll be able to restate the universal property of map without relying on monoid homomorphisms.
Filter
The filter function is a small step up in complexity from map, but its universal property is almost exactly the same. Again filter can be viewed through the lens of a universal property for list monoids, because filter itself takes a predicate and produces a list monoid. We know this because filtering two lists by the same predicate and concatenating them is the same as concatenating them first and then filtering them. Indeed, the only difference here is that the diagram now looks like this
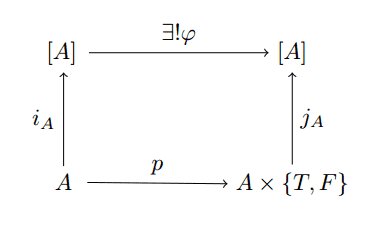
filter-bad
where $ p$ is our predicate, and $ j_A$ is defined by $ (a, T) \mapsto [a]$ and $ (a,F) \mapsto []$. The composition $ j_A \circ p$ gives the map $ A \to [A]$ that we can extend uniquely to a monoid homomorphism $ [A] \to [A]$. We won’t say any more on it, except to mention that again maintaining the order of the list is better described via fold.
Fold, and its Universal Property
Fold is different from map and filter in a very concrete way. Even though map and filter do specify that the order of the list should be preserved, it’s not an important part of their definition: filter should filter, and map should map, but no interaction occurs between different entries during the computation. In a sense, we got lucky that having everything be monoid homomorphisms resulted in preserving order without our specific intention.
Because it doesn’t necessarily produce lists and the operation can be quite weird, fold cannot exist without an explicit description of the order of operations. Let’s recall the definition of fold, and stick to the “right associative” order of operations sometimes specified by calling the function “foldr.” We will use foldr and fold interchangeably.
fun foldr(_, v, nil) = v
| foldr(f, v, (head::tail)) = f(head, foldr(f, v, tail))
Even more, we can’t talk about foldr in terms of monoids. Even after fixing $ f$ and $ v$, foldr need not produce a monoid homomorphism. So if we’re going to find a universal property of foldr, we’ll need a more general categorical picture.
One first try would be to view foldr as a morphism of sets
$$\displaystyle B \times \textup{Hom}(A \times B, B) \to \textup{Hom}([A], B)$$The mapping is just $ f,b \mapsto \textup{foldr } f \textup{ } b$, and this is just the code definition we gave above. One might hope that this mapping defines an isomorphism in the category of types and programs, but it’s easy to see that it does not. For example, let
$$A = \left \{ 1 \right \}, B = \left \{ 1,2 \right \}$$Then the left hand side of the mapping above is a set of size 8 (there are eight ways to combine a choice of element in $ B$ with a map from $ A \times B \to B$). But the right hand size is clearly infinite. In fact, it’s uncountably infinite, though not all possible mappings are realizable in programs of a reasonable length (in fact, very few are). So the morphism can’t possibly be a surjective and hence is not an isomorphism.
So what can we say about fold? The answer is a bit abstract, but it works out nicely.
Say we fix a type for our lists, $ A$. We can define a category $ \mathbf{C}_A$ which has as objects the following morphisms
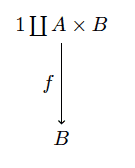
fold objects
By $ 1$ we mean the type with one value (null, if you wish), and $ f$ is a morphism from a coproduct (i.e. there are implicit parentheses around $ A \times B$). As we saw in our post on universal properties, a morphism from a coproduct is the same thing as a pair of functions which operates on each piece. Here one operates on $ 1$ and the other on $ A \times B$. Since morphisms from $ 1$ are specified by the image of the sole value $ f(1) = b$, we will often write such a function as $ b \amalg h$, where $ h: A \times B \to B$.
Now the morphisms in $ \mathbf{C}_A$ are the pairs of morphisms $ \varphi, \overline{\varphi}$ which make the following diagram commute:
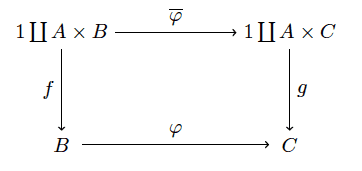
fold morphims
Here we write $ \overline{\varphi}$ because it is determined by $ \varphi$ in a canonical way. It maps $ 1 \to 1$ in the only way one can, and it maps $ (a,b) \mapsto (a, \varphi(b))$. So we’re really specifying $ \varphi$ alone, but as we’ll see it’s necessary to include $ \overline{\varphi}$ as well; it will provide the “inductive step” in the definition of fold.
Now it turns out that fold satisfies the universal property of being initial in this category. Well, not quite. We’re saying first that the following object $ \mathscr{A}$ is initial,
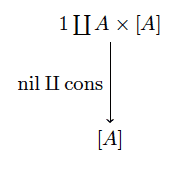
initial object fold
Where cons is the list constructor $ A \times [A] \to [A]$ which sends $ (a_0, [a_1, \dots, a_n]) \mapsto [a_0, a_1, \dots, a_n]$. By being initial, we mean that for any object $ \mathscr{B}$ given by the morphism $ b \amalg g: 1 \coprod A \times B \to B$, there is a unique morphism from $ \mathscr{A} \to \mathscr{B}$. The “fold” is precisely this unique morphism, which we denote by $ (\textup{fold g, b})$. We implicitly know its “barred” counterpart making the following diagram commute.
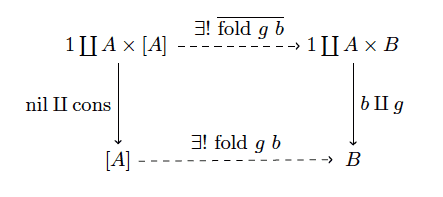
fold-univ-property
This diagram has a lot going on in it, so let’s go ahead and recap. The left column represents an object $ \mathscr{A}$ we’re claiming is initial in this crazy category we’ve made. The right hand side is an arbitrary object $ \mathscr{B}$, which is equivalently the data of an element $ b \in B$ and a mapping $ g: A \times B \to B$. This is precisely the data needed to define fold. The dashed lines represent the unique morphisms making the diagram commute, whose existence and uniqueness is the defining property of what it means for an object to be initial in this category. Finally, we’re claiming that foldr, when we fix $ g$ and $ b$, makes this diagram commute, and is hence the very same unique morphism we seek.
To prove all of this, we need to first show that the object $ \mathscr{A}$ is initial. That is, that any two morphisms we pick from $ \mathscr{A} \to \mathscr{B}$ must be equal. The first thing to notice is that the two objects $ 1 \coprod A \times [A]$ and $ [A]$ are really the same thing. That is, $ \textup{nil} \amalg \textup{cons}$ has a two-sided inverse which makes it an isomorphism in the category of types. Specifically, the inverse is the map $ \textup{split}$ sending
$ \textup{nil} \mapsto \textup{nil}$
$$[a_1, \dots, a_n] \mapsto (a_1, [a_2, \dots, a_n])$$So if we have a morphism $ \varphi, \overline{\varphi}$ from $ \mathscr{A} \to \mathscr{B}$, and the diagram commutes, we can see that $ \varphi = (b \amalg g) \circ \overline{\varphi} \circ \textup{split}$. We’re just going the long way around the diagram.
Supposing that we have two such morphisms $ \varphi_1, \varphi_2$, we can prove they are equal by induction on the length of the input list. It is trivial to see that they both must send the empty list to $ b$. Now suppose that for lists of length $ n-1$ the two are equal. Given a list $ [a_1, \dots, a_n]$ we see that
$$\displaystyle \varphi_1([a_1, \dots, a_n]) = \varphi_1 \circ \textup{cons} (a_1, [a_2, \dots, a_n]) = g \circ \overline{\varphi_1} (a_1, [a_2, \dots, a_n])$$where the last equality holds by the commutativity of the diagram. Continuing,
$$\displaystyle g \circ \overline{\varphi_1} (a_1, [a_2, \dots, a_n]) = g (a_1, \varphi_1([a_2, \dots, a_n])) = g(a_1, \varphi_2(a_2, \dots, a_n))$$where the last equality holds by the inductive hypothesis. From here, we can reverse the equalities using $ \varphi_2$ and it’s “barred” version to get back to $ \varphi_2([a_1, \dots, a_n])$, proving the equality.
To show that fold actually makes the diagram commute is even simpler. In order to make the diagram commute we need to send the empty list to $ b$, and we need to inductively send $ [a_1, \dots, a_n]$ to $ g(a_1, (\textup{fold g b})([a_2, \dots, a_n]))$, but this is the very definition of foldr!
So we’ve established that fold has this universal property. It’s easy now to see how map and filter fit into the picture. For mapping types $ A$ to $ C$ via $ f$, just use the type $ [C]$ in place of $ B$ above, and have $ g(a, L) = \textup{cons}(f(a), L)$, and have $ b$ be the empty list. Filter similarly just needs a special definition for $ g$.
A skeptical reader might ask: what does all of this give us? It’s a good question, and one that shouldn’t be taken lightly because I don’t have an immediate answer. I do believe that with some extra work we could use universal properties to give a trivial proof of the third homomorphism theorem for lists, which says that any function expressible as both a foldr and a foldl can be expressed as a list homomorphism. The proof would involve formulating a universal property for foldl, which is very similar to the one for foldr, and attaching the diagrams in a clever way to give the universal property of a monoid homomorphism for lists. Caveat emptor: this author has not written such a proof, but it seems likely that it would work.
More generally, any time we can represent the requirements of a list computation by an object like $ \mathscr{B}$, we can represent the computation as a foldr. What good does this do us? Well, it might already be obvious when you can and can’t use fold. But in addition to proving when it’s possible to use fold, this new perspective generalizes very nicely to give us a characterization of arbitrary computations on compound data types. One might want to know when to perform fold-like operations on trees, or other sufficiently complicated beasts, and the universal property gives us a way to see when such a computation is possible.
That’s right, I said it: there’s more to the world than lists. Shun me if you must, but I will continue dream of great things.
In an effort to make the egregiously long posts on this blog slightly shorter, we’ll postpone our generalization of the universal property of fold until next time. There we’ll define “initial algebras” and show how to characterize “fold-like” computations any compound data type.
Until then!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.