The Blessing of Distance
We have often mentioned the idea of a “metric” on this blog, and we briefly described a formal definition for it. Colloquially, a metric is simply the mathematical notion of a distance function, with certain well-behaved properties. Since we’re now starting to cover a few more metrics (and things which are distinctly not metrics) in the context of machine learning algorithms, we find it pertinent to lay out the definition once again, discuss some implications, and explore a few basic examples.
The most important thing to take away from this discussion is that not all spaces have a notion of distance. For a space to have a metric is a strong property with far-reaching mathematical consequences. Essentially, metrics impose a topology on a space, which the reader can think of as the contortionist’s flavor of geometry. We’ll explore this idea after a few examples.
On the other hand, from a practical standpoint one can still do interesting things without a true metric. The downside is that work relying on (the various kinds of) non-metrics doesn’t benefit as greatly from existing mathematics. This can often spiral into empirical evaluation, where justifications and quantitative guarantees are not to be found.
Metrics and Metric Spaces
Given a set $ X$, we say $ X$ is a metric space if it comes equipped with a special function $ d(x,y)$ that can compute the distance between any two points $ x,y$ of $ X$. Specifically, $ d$ must satisfy the axioms of a metric.
Definition: A function $ d: X \times X \to \mathbb{R}$ is a metric if it satisfies the following three properties for any choice of elements $ x, y, z \in X$.
- $ d(x,y) \geq 0$ (non-negativity), and $ d(x,y) = 0$ if and only if $ x=y$.
- $ d(x,y) = d(y,x)$ (symmetry)
- $ d(x,y) + d(y,z) \geq d(x,z)$ (triangle inequality)
Our goal now is to convince the reader that these three axioms are sensible for every notion of distance to satisfy. The first bullet claims that the distance between any two things can never be negative (hence called “non-negativity”), and that the distance between two things can only be zero if those two things are actually the same thing. The second bullet is a matter of perspective; the distance function reads, “the distance between $ x$ and $ y$,” and this shouldn’t change based on which element comes first in the sentence. This is the “symmetry” condition.
If one wants to prove a function is a metric, the third bullet is often the hardest property to establish. It’s called the triangle inequality, and in words it says that the lengths of edges of triangles make sense if you measure them with $ d$. Thinking of $ x, y, z$ as the vertices of a triangle, such as the one at left, we don’t want the length of one edge to be longer than the combined lengths of the other two edges. It’s a basic fact of Euclidean geometry that such a triangle cannot be drawn.

Walking from one vertex to another has an obviously shortest route: the straight line path
Pedantically, we notice that the third bullet above uses $ \geq$, which includes that $ d(x,y) + d(y,z) = d(x,z)$. It is not hard to see that this occurs (in Euclidean space, at least) when $ y$ lies on the line segment between $ x$ and $ z$. In this case it’s not truly a triangle, but it’s just convenient to pack it under the same name.
Aside from analyzing the abstract properties of a metric, the best way to understand this definition is to explore lots and lots of examples.
Of Norms and Graphs and Levenshtein, of Taxicabs and Kings
The simplest metric one could construct is called the discrete metric. It is defined by $ d(x,y) = 0$ if $ x = y$ and $ d(x,y) = 1$ otherwise. The symmetry and non-negativity conditions are trivially satisfied, and the triangle inequality is easy to prove. If $ d(x,y) + d(y,z) < d(x,z) \leq 1$, then it must be that $ x \neq z$, but both $ x=y$ and $ y=z$. The transitivity of equality, however, implies $ x=z$, a contradiction.
The discrete metric is completely useless for practical purposes, because all it can do is tell one that two things are equal or not equal. We don’t need a metric to do this in real life. On the other hand, mathematically this metric has a lot of uses. It serves as a conveniently pathological counterexample allowing one to gauge the plausibility of purported theorems in topology. These sorts of things usually only show up in the realm of point-set topology, which we haven’t breached yet on this blog, so we’ll leave it as a relevant link for now (hit the first link to page 41).
The most well known metric by far is the Euclidean metric. In $ n$ dimensions, this is just
$$\displaystyle d((x_1, \dots, x_n), (y_1, \dots, y_n)) = \sqrt{(y_1 – x_1)^2 + \dots + (y_n – x_n)^2}$$The non-negativity and symmetry of this metric follow from the fact that $ (a – b)^2 = (b – a)^2 \geq 0$ for all real numbers $ a,b$. The triangle inequality is a bit more difficult to prove, and without using a cop-out like Minkowski’s inequality, one would need to prove the pythagorean theorem for $ \mathbb{R}^n$, which implies the Cauchy-Schwarz inequality, which in turn implies the triangle inequality. Instead, we will do this at the end of this primer for a general vector space and a general inner product. The special case of the usual Euclidean dot product (which induces the Euclidean metric as above) will follow trivially.
The next metric we will inspect is the taxicab metric, also known as the Manhattan metric for the way it mimics driving distances on a grid of streets.
The picture below illustrates this: the green line represents usual Euclidean distance between the two black dots, while the blue, red, and yellow lines all represent the same distance via the taxicab metric. In particular, the distance is the sum of the lengths of the individual line segments, and it’s easy to see that the choice of path is irrelevant.
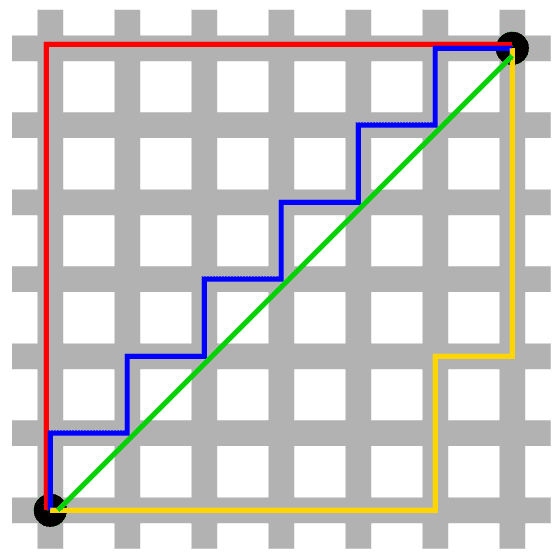
The red, yellow, and blue lines are all paths of equal length from the bottom left to the top right.
To make this more rigorous mathematically, we will pick the simplest possible path (the red one) to see that the distance is simply the sum of the differences of the x- and y-coordinates in absolute value. This generalizes to the following formula for arbitrary dimension.
$$\displaystyle d((x_1, \dots, x_n), (y_1, \dots, y_n)) = |x_1 – y_1| + |x_2 – y_2| + \dots + |x_n – y_n|$$For reasons the measure-theorist is familiar with, this metric is sometimes called the $ L_1$ metric. Much like the Euclidean metric, it also arises from a vector space (albeit not in the usual way). This function is non-negative and symmetric for the same reasons the Euclidean metric is. We will again defer the proof of the triangle inequality to the end of this post.
Next, we have the maximum metric, also known as the Chebyshev metric, which measures the distance it takes a king to travel from one point on a chessboard to another.
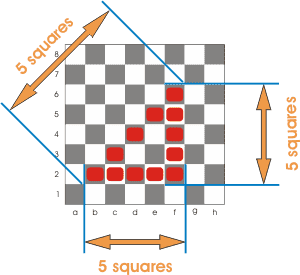
The picture to the left shows this in action. In particular, the distance required for a king to move from one square to another is exactly the maximum of the horizontal and vertical distances between the two squares.
If we generalized the chessboard and king’s movement rules to an arbitrary number of dimensions, it would result in taking the maximum of $ |x_i – y_i|$ over each coordinate indexed by $ i$.
Rigorously written, the maximum metric is defined by
$$\displaystyle d(x,y) = \max_i (|x_i – y_i|)$$As usual, symmetry and non-negativity are completely obvious. The triangle inequality is not so hard here. If $ z = x + y$, then
$ \max_i |z_i| = \max_i |x_i + y_i| \leq \max_i (|x_i| + |y_i|) \leq \max_i |x_i| + \max_i |y_i|$.
This is the distance between $ z$ and 0, and the more general result follows by translating the points in question (and it is easy to see that translation preserves distance).
Next, we can construct a metric on any undirected, weighted (or unweighted) graph $ G$, and we naturally call it the graph metric. The space is the set of vertices in $ G$, and the distance between two vertices is the shortest path between them, as per the weighting. In the case that $ G$ is unweighted, we can equivalently count the number of edges in the shortest path (shortest by edge count) or assume all edge weights are equal to 1. By virtue of being undirected and weights being non-negative, the symmetry and non-negativity conditions are trivially satisfied. The triangle inequality is (unusually) trivial as well. For if the shortest path from $ x$ to $ z$ were longer than the paths from $ x$ to $ y$ and $ y$ to $ z$ for some other vertex $ y$, then the latter is shorter than the former, a contradiction. For those readers familiar with group theory, this idea extends naturally to the metrics on groups, using the Cayley graph.
The last example is one we’ve explored at length on this blog, and that is the Levenshtein metric on words. Overly rigorously, it is a metric on a free monoid where we allow substitutions, insertions, and deletions. The reader is encouraged to read more about it in our post on metrics on words. An even simpler version of this is called the Hamming distance, where we only allow substitutions and the two words being compared must have the same length.
A Few Vague Words on Topology
As we have mentioned briefly before on this blog, a notion of distance allows one to consider any geometric construction that relies only on distance. The easiest examples are circles and ellipses, but one can also talk about convergent sequences, and other more analytic ideas.
But more importantly to mathematicians, metrics generate very tractable topologies. While we’re not suited to begin a full-blown discussion of topology in this primer, we will at least say that a topology is simply a definition of open sets, subject to appropriate properties. For a metric, open sets are usually defined again by circles. That is, one might define the open sets to be all the unions and finite intersections of open disks, where an open disk is a set of the form $ \left \{ y : d(x,y) < C \right \}$ for some center $ x$, and some constant $ C$.
The structure induced by these open sets is very flexible. In particular, two topological spaces are said to be equivalent if a function between them preserves open sets in both directions. This allows for all sorts of uncanny stretching and bending, such as those used to turn a sphere inside-out. The formal word for such a function is a homeomorphism, and the two spaces are said to be homeomorphic. One would be right to think that without certain assumptions, topologies could be wild and crazy beyond our imagination. The important point for this post is that a topology coming from a metric space is particularly well-behaved (at least as far as topologies go), satisfying a number of helpful properties for their analysis.
While it might seem weird and arbitrary to talk of open sets as a “structure” of a space, it turns out to yield a very rich theory and surprising applications. We plan to explore some of these applications on this blog in the distant future.
Inner Product Spaces: a Reprise
In what follows we will give a detailed but elementary treatment of the triangle inequality for a general inner product space. One should note that there are even more general spaces that allow for metrics with the triangle inequality, but these usually involve measure theory or take the triangle inequality as an axiom. In this post, we want to see the triangle inequality occur as a result of the existence of an inner product. For a refresher on inner product spaces and the basic definitions, the reader should refer to our primer on the subject.
Before we continue, we should also note which inner products induce which metrics. For the Euclidean metric it is obviously the Euclidean inner product. For the taxicab metric one should refer to Wikipedia.
Let $ V$ be an inner product space, and let $ v \in V$. We define the norm of $ v$ to be $ \| v \| = \sqrt{\left \langle v,v \right \rangle}$. This coincides with the usual Euclidean norm if we use the Euclidean inner product, and the $ L_p$ norm if we use the appropriate integral inner product.
There are some trivial properties one would expect to be true of norms, such as non-negativity, $ \| v \| = 0$ if and only if $ v = 0$, and $ \| av \| = |a| \| v \|$ for scalars $ a$. We leave these as exercises to the reader.
As we noted in our primer on inner product spaces, two vectors $ v,w$ are said to be orthogonal if $ \left \langle v,w \right \rangle = 0$. From this we can prove the Pythagorean Theorem for an inner product space.
Theorem: If $ u,v$ are orthogonal vectors, then $ \| u + v \|^2 = \| u \|^2 + \| v \|^2$.
Proof. By definition, $ \| u + v \|^2 = \left \langle u+v, u+v \right \rangle$, and this expands by linearity of the inner product to
$$\displaystyle \|u \|^2 + \| v \|^2 + \left \langle u,v \right \rangle + \left \langle v,u \right \rangle$$As the two vectors are orthogonal, the right two terms are zero, giving the desired result. $ \square$
Now given a vector $ v$, we describe a useful way to decompose another vector $ u$ into two parts, where one is orthogonal to $ v$ and one is a scalar multiple of $ v$. A simple computation gives a unique result:
$$\displaystyle u = \frac{\left \langle u,v \right \rangle}{\| v \|^2}v + \left ( u – \frac{\left \langle u,v \right \rangle}{\|v \|^2}v \right )$$We call the first term the projection of $ u$ onto $ v$. The second term is then simply the remainder after subtracting off the projection. This construction helps us understand the relationship between two vectors, but it also helps us understand the relationship between the inner product and the norm, as in the following theorem.
Theorem: (The Cauchy-Schwarz Inequality). For all $ u,v \in V$,
$ | \left \langle u,v \right \rangle | \leq \|u \| \|v \|$.
Proof. If $ v=0$ then the inequality trivially holds, so suppose $ v \neq 0$. Consider the square norm of the orthogonal decomposition of $ u$ onto $ v$, where we denote the orthogonal part by $ w$.
$$\displaystyle u = \frac{\left \langle u,v \right \rangle}{\| v \|^2}v + w$$By the Pythagorean Theorem, we have
$$\displaystyle \| u \|^2 = \left \| \frac{\left \langle u,v \right \rangle}{\| v \|^2}v \right \|^2 + \| w \|^2$$Since the scalar multiples pass squared through the norm, this is the same as
$$\displaystyle \| u \|^2 = \frac{|\left \langle u,v \right \rangle |^2}{\| v \|^2} + \|w \|^2$$Since norms are non-negative, we can omit the $ w$ part and get an inequality
$ \displaystyle \| u \|^2 \geq \frac{| \left \langle u,v \right \rangle |^2}{\| v \|^2}$.
Multiplying both sides by $ \| v \|^2$ and taking square roots gives the result. $ \square$
And now we may finally get to the triangle inequality for norms, which says that $ \| u + v \| \leq \| u \| + \| v \|$. Before we prove this, note that we can bring this back to the world of metrics by defining a metric based on the norm as $ d(u,v) = \| u-v \|$, and the statement about the triangle inequality translates to what we expect it should. So concluding this primer we present the proof of the triangle inequality.
Theorem: For all $ u,v \in V, \| u+v \| \leq \| u \| + \| v \|$.
Proof. Expanding $ \| u + v \|^2$ using the properties of the inner product we get
$$\displaystyle \| u + v \|^2 = \| u \|^2 + \| v \|^2 + 2 \textup{Re}\left \langle u,v \right \rangle$$Where “Re” stands for the real part of the (possibly complex-valued) inner product. As the real part bounded by the complex absolute value, we introduce our first inequality as
$$\displaystyle \| u +v \|^2 \leq \| u \|^2 + \| v \|^2 + 2|\left \langle u,v \right \rangle|$$By the Cauchy-Schwarz inequality, the last term is bounded by the norms of $ u$ and $ v$, giving
$$\displaystyle \| u+v \|^2 \leq \| u \|^2 + \| v \|^2 + 2 \| u \| \| v \| = (\| u \| + \| v \|)^2$$And taking square roots gives the result. $ \square$
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.