
Problem: Prove that generalized versions of Mario Brothers, Metroid, Donkey Kong, Pokemon, and Legend of Zelda are NP-hard.
Solution: http://arxiv.org/abs/1203.1895v1
Discussion: Three researchers (including Erik Demaine, a computer science professor at MIT famous for his work with the mathematics of origami) recently finished a paper giving the complexity of a number of classic Nintendo games (the ones I loved to play). All are proven NP-hard, some are shown to be NP-complete, and some are PSPACE-complete. Recall, a problem is NP-hard if an NP-complete problem reduces to it, and a problem is NP-complete if it’s NP-hard and also in NP. As we have just posted a primer on NP-completeness and reduction proofs, this paper is a fun next step for anyone looking for a more detailed reduction proof. A pre-print is available for free on arXiv, and it’s relatively short and easy to read. I’ll summarize his result here, and leave most of the details to the reader. Each game is “generalized” to the task of determining whether one can get from a “start” location to a “finish” location. So the decision problem becomes: given a finite level of a game, can the player move from the starting location to the finishing location? All of the reduction proofs are from 3-Sat, and they all rely on a common framework which can be applied to any platform game. Pictorially, the framework looks like this:
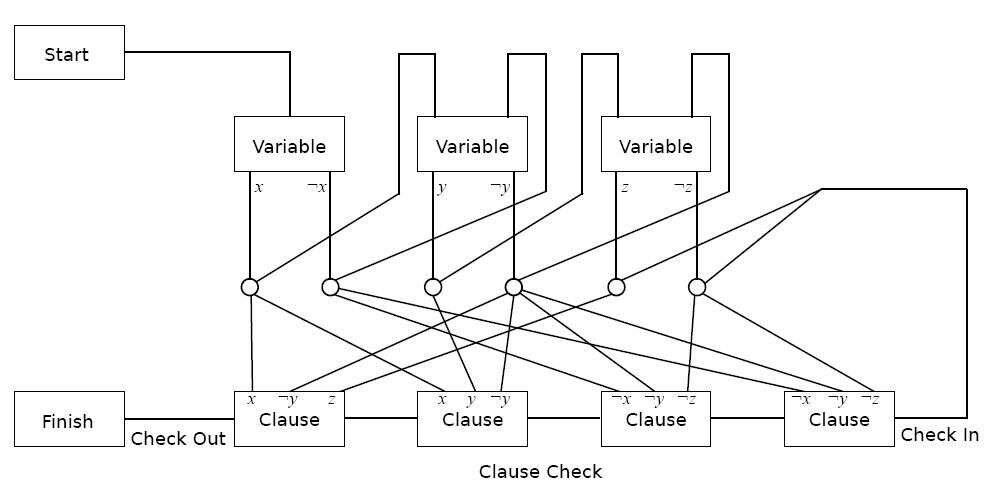
The player starts in the “start” gadget, which allows one to set up initial state requirements. For instance, in Super Mario Brothers, the start provides you with a mushroom, and you cannot get to the finish without being able to break blocks by jumping under them, which requires the mushroom power-up. Each “variable” gadget requires the player to make a variable assignment in such a way that the player can never return to that gadget to make a different decision. Then each “clause” gadget can be “unlocked” in some way, and each clause gadget can only be visited by the player once the player has chosen a satisfying variable assignment for that clause. Once the player has visited all variable gadgets, he goes to the “check in” area, and can travel back through all of the clauses to the finish if and only if he unlocked every clause. The crossover of the paths in the picture above requires another gadget to ensure that the player cannot switch paths (the details of this are in the paper).
For example, here is the variable gadget described in the paper for The Legend of Zelda, a Link to the Past:

Note that here we require Link has the hookshot, which can grapple onto chests, but has limited reach. The configuration of the chests requires him to choose a path down one of the two columns at the bottom, and from there he may never return.
Here’s another example. In the classic Super Mario Brothers game, a possible clause gadget is as follows.

Note that if the player can only enter through one of the three columns at the top, then the only thing he can do is kick a red koopa shell down so that it breaks the blocks, unlocking the way for Mario to pass underneath at the end. Note that Mario cannot win if he falls from the top ledge (since must always remain large, he can’t fit through a one-tile-high entryway). Further details include the hole at the bottom, in which any stray koopa shell will necessarily fall, but which Mario can easily jump over. We recommend reading the entire paper, because it goes into all of the necessary details of the construction of the gadgets for all of the games.
Future Work
We note that there are some parts of the paper that only got partial results, mostly due to the variation in the game play between the different titles. For instance, the original Super Mario Brothers is known to be NP-complete, but the added ability to pick up koopa shells in later Super Mario Brothers games potentially makes the decision problem more complex, and so it is unknown whether, say, Super Mario World is in NP. We will summarize exactly what is known in the table below. If readers have additions for newer games (for instance, it’s plausible that Super Mario Galaxy could be adapted to fit the same construction as the original Super Mario Bros.), please leave a comment with justification and we can update the table appropriately. I admit my own unfamiliarity with some of the more recent games.
Super Mario Brothers:
| Game Title | NP-hard | in NP | PSPACE-complete |
|---|---|---|---|
| Donkey Kong | |||
| Donkey Kong Country | ✓ | ✓ | |
| Donkey Kong Land | ✓ | ✓ | |
| Country 2: Diddy’s Kong Quest | ✓ | ✓ | |
| Land 2 | ✓ | ✓ | |
| Country 3: Dixie Kong’s Double trouble! | ✓ | ✓ | |
| Land 3 | ✓ | ✓ | |
| Donkey Kong 64 | |||
| Donkey Kong Country Returns |
Metroid:
| Game Title | NP-hard | in NP | PSPACE-complete |
|---|---|---|---|
| Metroid | ✓ | ✓ | |
| Metroid II: Return of Samus | |||
| Super Metroid | ✓ | ✓ | |
| Fusion | |||
| Prime | ✓ | ✓ | |
| Prime 2: Echoes | |||
| Prime Hunters | ✓ | ✓ | |
| Prime 3: Corruption | ✓ | ✓ | |
| Other M | ✓ | ✓ |
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.