Problem: Show that $ \sqrt{2}$ is an irrational number (can’t be expressed as a fraction of integers).

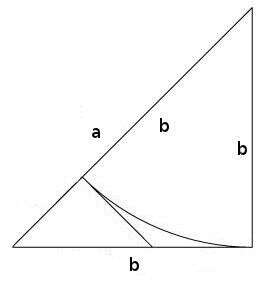
Solution: Suppose to the contrary that $ \sqrt{2} = a/b$ for integers $ a,b$, and that this representation is fully reduced, so that $ \textup{gcd}(a,b) = 1$. Consider the isosceles right triangle with side length $ b$ and hypotenuse length $ a$, as in the picture on the left. Indeed, by the Pythagorean theorem, the length of the hypotenuse is $ \sqrt{b^2 + b^2} = b \sqrt{2} = a$, since $ \sqrt{2} = a/b$.

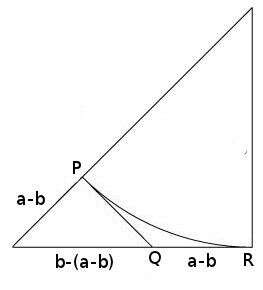
Swinging a $ b$-leg to the hypotenuse, as shown, we see that the hypotenuse can be split into parts $ b, a-b$, and hence $ a-b$ is an integer. Call the point where the $ b$ and $ a-b$ parts meet $ P$. If we extend a perpendicular line from $ P$ to the other leg, as shown, we get a second, smaller isosceles right triangle. Since the segments $ PQ$ and $ QR$ are symmetrically aligned (they are tangents to the same circle from the same point), they too have length equal to $ a-b$. Finally, we may write the hypotenuse of the smaller triangle as $ b-(a-b) = 2b-a$, which is also an integer.

So the lengths of the sides of the smaller triangle are integers, but by triangle similarity, the hypotenuse to side-length ratios are equal: $ \sqrt{2} = a/b = (2b-a)/(a-b)$, and obviously from the picture the latter numerator and denominator are smaller numbers. Hence, $ a/b$ was not in lowest terms, a contradiction. This implies that $ \sqrt{2}$ cannot be rational. $ \square$

This proof is a prime example of the cooperation of two different fields of mathematics. We just translated a purely number-theoretical problem into a problem about triangle similarity, and used our result there to solve our original problem. This technique is widely used all over higher-level mathematics, even between things as seemingly unrelated as topological curves and groups. Finally, we leave it as an exercise to the reader to extend this proof to a proof that whenever $ k$ is not a perfect square, then $ \sqrt{k}$ is irrational. The proof is quite similar, but strays from nice isosceles right triangles