Geometric Series with Geometric Proofs

Problem: $ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots = 1$

Solution:

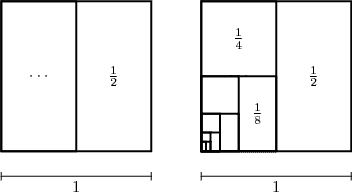
Problem: $ \frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \dots = \frac{1}{2}$

Solution:

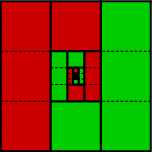
Problem: $ \frac{1}{4} + \frac{1}{16} + \frac{1}{64} + \dots = \frac{1}{3}$

Solution:

Problem: $ 1 + r + r^2 + \dots = \frac{1}{1-r}$ if $ r < 1$.

Solution:

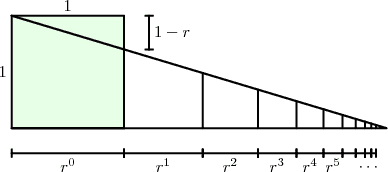
This last one follows from similarity of the subsequent trapezoids: the right edge of the teal(ish) trapezoid has length $ r$, and so the right edge of the neighboring trapezoid, $ x$, is found by $ \frac{r}{1} = \frac{x}{r}$, and we see that it has length $ r^2$.

We may come up with infinitely many proofs of these geometric series! All we need is a figure which can be dissected into $ n$ self-similar parts, where the geometric series is a sum of powers of $ \frac{1}{n}$. Awesome.