Determinism and Finite Automata—A Primer

The first step in studying the sorts of possible computations (and more interestingly, those things which cannot be computed) is to define exactly what we mean by a “computation.” At a high level, this is easy: a computation is simply a function. Given some input, produce the appropriate output.

Unfortunately this is much too general. For instance, we could define almost anything we want in terms of functions. Let $ f$ be the function which accepts as input the date of California Super Lotto drawings, and returns the set of winning numbers for that date. Of course (assuming the winning numbers are chosen randomly), this is ridiculous and totally uninformative. We cannot learn anything interesting about computations if they are performed behind an opaque veil. Instead, we need to rigorously define the innards of our model for computation, and then see what kinds of things it can do.

Because our inputs may be long and complicated, our model should break an input into pieces and work on the pieces in sequence. This motivates the following two definitions:

Definition: An alphabet is a finite set, usually denoted $ \Sigma$.

Definition: $ \Sigma^*$ is the set of finite strings whose characters come from $ \Sigma$. We include the empty string $ \varepsilon$ as the string of zero length. This operation is called the Kleene star.

We will henceforth let inputs to our model be elements of $ \Sigma^*$ for some fixed alphabet $ \Sigma$, and operate on each character one at a time.

Since $ \Sigma$ is finite, we may assign to each element a unique finite string of ones and zeros (to keep things simple, let each string have length equal to ceiling of $ \log |\Sigma|)$. Then, we can simulate any alphabet by the appropriate subset of $ \left \{0,1 \right \}^*$. So without loss of generality, we may always assume our input comes from $ \left \{ 0,1 \right \}^*$, and thus we will henceforth have $ \Sigma = \left \{ 0,1 \right \}$.

Now we need a clear objective for our model, and we will phrase it again in terms of $ \Sigma^*$. Specifically, we pick a subset of $ A \subset \Sigma^*$, and call it a language. Our computational model will accept an input, and output “accept” or “reject.” We say that our model recognizes $ A$ if it accepts and only accepts those strings in $ A$.

Notice that this is a bit different from our colloquial idea of “computation.” Specifically, all our model will do is determine presence of an element in a set which has a potentially complicated construction. While it at first seems that this does not include things like “adding two numbers,” it turns out that we may phrase such objectives in terms of acceptance and rejection. Let $ A = \left \{ axbxc | a,b,c \in \mathbb{N}, a+b=c \right \}$, where $ x$ is some fixed separator. If we fix $ a$ and $ b$, then we may run our computational model on successively higher values of $ c$ (ordered by absolute value, or restricting everything to be positive) until finding acceptance.

Colloquially, we have defined “computation” as recognizing all inputs which satisfy a qestion. Moreover, we will see that very many complex problems can be recognized as recognition problems, including things that are logically impossible to compute within our model.

The reason we have been heretofore vague in naming our model is that we will actually define four different models of progressively stronger computational ability, and this framework will hold for all of them. So here our first try.

Deterministic Finite Automata

This definition comes from the intuitive idea that a computation can be carried out via a set of states and transitions between those states. A very simple example is a light switch, which has the states ‘on’ and ‘off’, and which can accept as input ‘switch’ or ‘do nothing’. This model is rigorized here:

Definition: A deterministic finite automaton, abbreviated DFA, is a five-tuple $ D = (S, \Sigma, \tau, s_0, F)$, where:

• $ S$ is a set of states, with initial state $ s_0$.
• $ \Sigma$ is our working alphabet, and inputs come from $ \Sigma^*$.
• $ \tau$ is a transition function $ S \times \Sigma \to S$, which maps the current state and next input character to the next appropriate state.
• $ F \subset S$ is a set of final states. If the last input character lands us in any state $ f \in F$, we accept.

Rigorously, let our input word $ w \in \Sigma^*$ have length $ n$ and characters indexed $ w_k$. Call the sequence of states in the computation $ s_k$, where $ s_{k+1} = \tau(s_k, w_k)$. Then our DFA accepts $ w$ if and only if $ s_n \in F$. We will use this notation throughout our discussion of finite automata. We call the set of languages which a DFA can recognize the regular languages. We will soon see that this class is rather small.

Of course, we have some examples of DFAs. The simplest possible DFA has only one state, $ s$, and the transition function $ \tau(s,a) = s$ for all $ a \in \Sigma$. Depending on whether $ F$ is empty, this DFA will accept or reject all of $ \Sigma^*$. We may visualize this DFA as a directed graph:

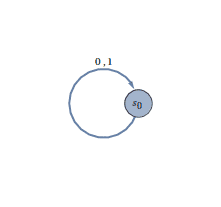
Indeed, this visualization provides a convenient way for us to write out the transition function. We simply draw an edge originating at each state for each element of our alphabet. When two or more inputs have the same behavior, we label one edge with multiple input symbols, as above.

Here is a more interesting example: let $ A$ be the set of binary strings which have an even number of zeros. We design a DFA to accept this as follows:

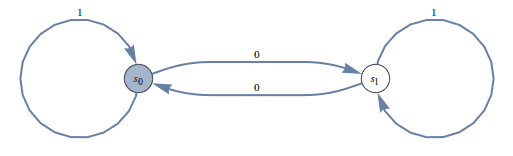
The shaded state, $ s_0$ is the only final state. It is obvious from tracing the diagram that this DFA accepts precisely the set of strings with evenly many zeros. Let’s try something harder:

Let $ A = \left \{ 0^n1^n | n \in \mathbb{N} \right \}$. This is a simple enough language, so let us develop a DFA to recognize it. We can easily construct a DFA which recognizes $ 0^n1^n$ for a fixed $ n$, and if we have two DFAs we can construct a DFA which recognizes their union quite easily (do so as an exercise!). However, due to the restriction that $ S$ is finite, we cannot connect these pieces together indefinitely! While we might imagine some cleverly designed DFA exists to recognize $ A$, we find it more likely that no such DFA exists.

Indeed, it has been proven that no such DFA exists. The key to the proof lies in an esoteric lemma called the Pumping Lemma. Being a notational beast of a lemma, we will not state it rigorously. Colloquially, the lemma says that if $ A$ is a regular language, then any sufficiently large word $ w \in A$ can be split up into three pieces $ xyz$, such that the middle piece may be repeated arbitrarily many times, as $ xyyyy \dots yz$, with the resulting word still being in $ A$. Clearly this breaks the “balance” restraint of $ A$ no matter where the splitting is done, and so $ A$ cannot be regular.

Before we increase our model’s expressive power, let us make an “enhancement” to the DFA.

Nondeterministic Finite Automata

Following the colloquial definition of nondeterminism, we can design our computational system to make state transitions “branch out.” This will be made clear by a slight modification of the DFA.

Definition: A nondeterministic finite automaton, abbreviated NFA, is a DFA with the following two modifications:

• Instead of having a single state $ s_k$ at each step, we allow a set of possible states, which we denote $ S_k \subset S$.
• Our initial state $ s_0$ is replaced with an initial set of states $ S_0 \subset S$.
• We include $ \varepsilon$ in $ \Sigma$, allowing for immediate transitions that require no input.
• The transition function $ \tau$ now has signature $ S \times \Sigma \to P(S)$, where $ P(S)$ denotes the power set of $ S$, the set of all subsets of $ S$.
• At each step (with input character $ w_k$), we map $ \tau(-,w_k)$ over $ S_k$ to get $ S_{k+1}$, i.e. $ S_{k+1} = \left \{ \tau(s, w_k) | s \in S_k \right \}$
• The NFA accepts if any state in $ S_n$ is final.

In this way, our machine can get a character as input, and proceed to be in two separate states at the same time. If any of the branches of computation accept, then they all accept.

Extending our example from DFAs, here is an NFA which accepts the language of binary strings which have either an even number of zeros or an even number of ones (or both).

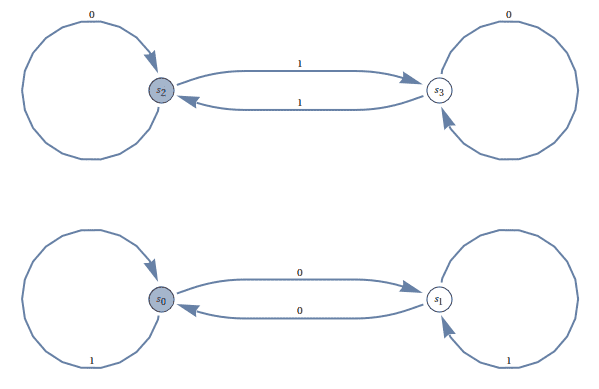
Here, $ S_0 = F = \left \{ s_0, s_2 \right \}$, and by tracing (a little more carefully this time), we can see that it accepts what we expect.

Now, with the added strength of nondeterminism, we might expect that NFAs can compute some things that DFAs cannot. Amazingly, this is not the case. We point the reader to a more detailed description, but trust that our quick explanation will give the necessary intuition to see the equivalence.

The key observation is that despite nondeterminism, there is still a finite number of possible states an NFA can be in. Specifically, there are at most $ 2^{|S|}$ possible subsets of $ S$, so we can simply construct a DFA which has $ 2^{|S|}$ states, one corresponding to each subset of $ S$, and build up a deterministic transition function that makes things work. This would be an appropriate exercise for the advanced reader, but the beginning student should see Sisper’s Introduction to the Theory of Computation, which contains a complete and thorough proof. (We hate to refer the reader to an expensive textbook, but we could only find sparse proofs of this equivalence elsewhere on the internet, and most assume a particular working set of notation. And Sisper’s book is much better than this terse post for a primer in Computing Theory. The interested reader who lacks mathematical maturity would find it very accessible.)

In other words, every NFA has a corresponding DFA which recognizes precisely the same language. On the other hand, every DFA is trivially an NFA. Thus, the class of languages which NFAs recognize is also the regular languages.

So we have discovered that regular languages, and hence the DFAs and NFAs which recognize them, are quite limited in expressive power. Now let’s truly beef up our model with some mathematical steroids.

Pushdown Automata

Okay, so these steroids won’t be that strong. Ideally, we just want to add as little as possible to our model and still make it more expressive. This way we can better understand the nuances of computational power, thus strengthening our intuition. While “little” is a subjective notion, lots of “littler” things were tried before arriving at a model that was not equivalent in power to a DFA. We will refrain from explaining them here, except to say that DFAs are equivalent in power to the class of formal Regular Expressions (hence the name, regular languages), which most programmers are familiar with on an informal level.

Definition: A pushdown automaton, denoted PDA, is an NFA with two additional components: $ \Gamma$ a set of stack symbols including $ \varepsilon$, and a modified transition function $ \tau$:

Here, the left hand $ \Gamma$ symbol represents the current top of the stack (which is always popped), and the right hand $ \Gamma^*$ represents any modification to the stack during state transition. This modification is always a push, and can be an empty push, or a push of arbitrarily many symbols.

For brevity of a description of $ \tau$, which would otherwise be infinite as there are infinitely many possible stacks, we allow $ \tau$ to be a partial function, not defined for some inputs. Then a PDA automatically rejects any encountered undefined input. Alternatively, we could construct $ \tau$ as a total function, if we add edges for each undefined input going to some terminal state which is inescapable and not final. For the sake of this post, we will accept a partial transition function.

Recalling our discussion of computational ability in our post on Conway’s Game of Life, we recognize that a PDA’s new power is in its ability to grow without bound. Specifically, the stack has no limit to its size, and we can remember important pieces of input which would otherwise be discarded.

This modification seems like it was made just for the $ 0^n1^n$ problem. Specifically, now we can just push the 0s we see on to the stack, and pop just 1’s until we see an empty stack. Here is a PDA which does just that (making heavy use of epsilon transitions):

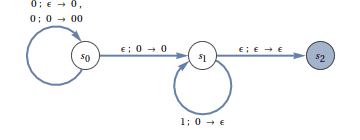
Here $ S_0 = \left \{ s_0 \right \}$, and $ F = \left \{ s_2 \right \}$. For each state transition label, we include $ w_k; a \to bc$ to mean, “upon receiving $w_k$ as input with $ a$ on top of the stack, pop $ a$ and replace it with $ bc$, where $ bc$ may be a single character or multiple characters or the empty character. The epsilon transitions allow us to move from $ s_0$ to $ s_1$ and from $ s_1$ to $ s_2$ seamlessly, but only when the stack is agreeable. As an exercise, modify the above diagram to instead recognize $ 0^{2n}1^n$.

Neato! It seems like we’ve got a huge boost in computational power now that we can store some information. Wrong. As great as a stack is, it’s not good enough. Here’s a language that a PDA cannot solve: $ A = \left \{ 0^n1^n2^n | n \in \mathbb{N} \right \}$. This follows from an additional and more nuanced pumping lemma, and we will not dwell on it here. But look at that! This language is hardly any more complex than $ 0^n1^n$, and yet it stumps our PDA.

Time to up the steroid dosage. Surprisingly enough, it turns out that our solution will be equivalent to adding another stack! In doing so, we will achieve a level of computational expression so powerful that nothing we know of today can surpass it. We call this panacea of computational woes a Turing machine, and we will cover both it and the wild problems it cannot compute next time.

Until then!