Turing Machines and Conway's Dreams

Additional Patterns

Last time we left the reader with the assertion that Conway’s game of life does not always stabilize. Specifically, there exist patterns which result in unbounded cell population growth. Although John Conway’s original conjecture was that all patterns eventually stabilize (and offered $50 to anyone who could provide a proof or counterexample), he was proven wrong. Here we have the appropriately named glider gun, whose main body oscillates, expelling a glider once per period. Here is an initial configuration:

And its animation:

This glider gun was the first one of its kind ever discovered. To distinguish it from the now large class of “gun” patterns, it is called Gosper’s glider gun. It has the smallest initial population of any known gun (hint, hint: find a smaller one and get famous!).

Second, we have examples of moving patterns which leave stationary patterns as they travel. These are commonly called puffers. For the sake of amazement, we give the coolest puffer we could find, which actually lays Gosper guns! (credit to Wikipedia for the image)

At the end of the animation, the red colored cells are the puffer, the green are Gosper guns, and the blue are the emitted gliders.

So (after the work of many in searching for these patterns), we see that under special circumstances Life can grow without bound. This has an interesting connection to computability. Specifically, any model of computation in which every computation is guaranteed to stop (in the case of cellular automata, this is reaching a stable state) cannot be Turing-complete.

[Note: the details on Turing machines are covered in this blog’s primer on the theory of computation, but the reader may recall that a system for computation which is Turing-complete can do any computation that can be done on any other Turing machine. This includes performing arithmetic, simulating Conway’s Game of Life, and performing the functions of a web browser.]

So colloquially, being able to simulate an infinite loop (or infinite recursion) is required to do interesting computations. More rigorously, if an automaton is to simulate a Turing machine, then it must be able to loop infinitely, because a Turing machine can.

But we have just found that Life can simulate infinite loops. Specifically, a Gopser gun or the puffer above both simulate an infinite counter, counting the number of emitted/laid patterns. Admittedly, we can’t do much with just an infinite counter, but it gives us the hint that we may be able to construct the elementary pieces of a real computation engine. We conjecture now that Life is Turing-complete, and will prove it by construction. While it would be amazing to fit such a proof in a blog post, in reality we will explain a sketch the proof, elaborate on certain parts, and defer to the large body of work already done on this problem to assert our claim.

Bits and Gates

Recall there is a sufficient pair of conditions for a computational model to be Turing-complete: the ability to implement arbitrary logic functions and the existence of a model for random access memory (the read-write tape and write head).

In standard computers, these logic functions are built up via elementary logic gates. High and low current, representing 1 and 0, respectively, are sent through the logic gates, which output the appropriate level of current corresponding to the logic function. The easiest set of complete logic gates are And, Or, and Not, from which any arbitrarily complex truth table can be built.

On the other hand, it is not hard to prove that the Nand (X Nand Y := Not (X And Y)) function alone is sufficient to implement all logic functions. And so in contemporary circuit design, Nand gates (which are cheap to manufacture) are used in the billions to implement all of the necessary logic in a computer chip.

Hence, the ability to simulate a complete set of logic gates in Life is necessary for its Turing-completeness. From our investigation of the patterns above, there is one obvious candidate for current: a Gosper gun. A stream of emitted gliders corresponds to high current, and an absence to low. We include a special “eater” stationary pattern which controls the current.

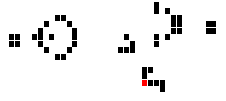
Further, another copy of this eater can be used to manage the output, and multiple eaters can be combined to handle two input streams, thus implementing logic. Indeed, the construction is very detailed, and requires a lot of tinkering to understand. Here we present the And gate, and send the reader to LogiCell for the designs of Or and Not.

A and B represent the input currents to the gate, while C is a continuous stream. The two eaters at bottom center allow a current to pass through if and only if the current hitting it comes from B and only B. Current coming from A collides with C, cancelling both streams. If A is off (as it is in the diagram above), then B cancels with C and the eaters simultaneously, and no gliders get through. If A is off but B is on, then A cancels with C, and B still does not hit get through. However, if A and B are both on, then everything works great.

So building up from the And, Or, and Not pieces, we may implement every possible logic function. Thus, as in the original proof of Life’s Turing-completeness, we can model a finite state machine attached to two counters, which itself is Turing-complete.

[The proof of the two-counter Turing-completeness is sketched as follows. Every Turing machine can be simulated by two stacks. i.e., If $ H$ is the position of the read-write head of a Turing machine, then the head of one stack corresponds to the values to the right of $ H$ including $ H$, while the second stack corresponds to the values strictly to the left of $ H$. Then, any stack can be simulated by two counters, where the bits of one counter are the bits in successive cells in the stack, and the second number is required extra space for stack operations. Hence, a two stack machine can be simulated by four counters. Finally, four counters may be simulated by two counters, where one counter contains a number $ x=2^a3^b5^c7^d$, where $ a,b,c,d$ correspond to the integer values of our four simulated counters, and the second counter is used in the arithmetic to modify $ x$. Therefore, one counter contains the information of all four stacks. Working backward, a finite state machine which can control two counters has the same computing power as a Turing machine. It is thus Turing-complete.]

A Gargantuan Pattern

Now, proving Turing-completeness and implementing a computing machine within Life are two very different things. For one thing, we require some system of registers and memory access. Amazingly enough, researchers have created fully universal Turing machines (which can simulate other Turing machines). We point the reader to a picture of the initial configuration for a small Turing machine and a very detailed description of its parts and instruction set.

The glorious promise of Turing-completeness must be taken with a grain of salt. If we were to run within Life some wonderful computation that we might actually find useful as human beings, it would probably take longer than the life of the sun to complete. Indeed, we don’t actually care about computational speed or the prettiness of its output. Our true goal was the theoretical proof that this model is equivalent in power to a Turing machine. This has a number of profound implications (most of which have been voiced before by the Big Names of mathematics).

Specifically, we initially started with a very simple set of rules. From this, we observed much chaotic behavior, but found some order in still patterns, gliders, and oscillators. After thoroughly mastering these pieces, we suddenly found the ability to compute anything that can be computed! All of this order was hiding in chaos.

Furthermore, given an infinite grid with random initial configuration, a Turing machine sub-pattern is guaranteed to exist in it with probability 1 (see the Infinite Monkey Theorem). Not only that, but there are guaranteed to exist sub-patterns corresponding the Turing machines for every possible computation. This includes the Facebook social graph, Halo 3, the proof of the Four Color Theorem, and every program that will ever be written in the future. All in the same grid.

So with the minuscule initial design of a few simple rules, and given enough randomness, there is guaranteed to be order and elegance of the most magnificent and mind-boggling nature. Not even in Conway’s wildest dreams would we find such beauty! This is a gem of mathematics. We leave it to the reader to extrapolate philosophy and debate theories of intelligent design; we are content to admire.

At some point in the future, we wish to investigate using genetic programming to search for “interesting” Life patterns. Furthermore, the idea came upon us to run a Life-like game with $ k-$regular cells where $ k$ is arbitrary. For large $ k$, tessellation of these cells is only possible in the hyperbolic plane, but with the appropriate geometric software, this may give an interesting visualization of a variant of Life where, say, each cell has eight, nine, or ten neighbors (hexagonal cells has been done, as tessellation is easy in the Euclidean plane). Of course, even though a hyperbolic tessellation is indeed infinite, the cells grow exponentially smaller as they near the edge of the plane, effectively restricting our working space. Implementing this variant would require a bit of research, so we will likely write on other topics in the mean time.

Until next time!